02 - Exercícios
Factorials and Powers of Two, Sudoku
Autor(es):
Resolução dos Exercícios
Exercícios: E e F
F - Factorials and Powers of Two
-
Um número é considerado powerful se:
- Potência de dois ou,
- Fatorial
-
ou seja, o número m é powerful se existe um inteiro d não negativo:
- m = 2^d ou,
- m = d!
-
Dado um valor n, encontre o mínimo número k tal que n possa ser representado como a soma de k números distintos que são powerful.
-
Exemplos:
240 = 24 + 32 + 64 + 120 (k = 4)
240 = 120 + 120 (INVÁLIDO)
7 = 1 + 2 + 4 (k = 3) 7 = 1 + 6 (k = 2) Solução: 2
- Se n não pode ser representado pela soma de distintos números powerful, print -1
- Essa situação nunca irá acontecer pois qualquer número inteiro pode ser representado pela soma de potências de dois.
-
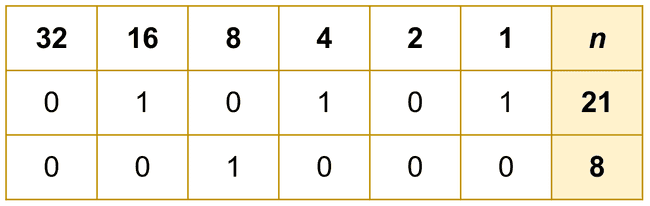
Sendo assim, a quantidade de bits ativos no número n como o mínimo valor para k.
-
A solução ótima pode ser formada por uma das seguintes situações:
-
Situação 1:
- Soma somente de valores potências de dois.
-
Situação 2:
- Soma somente de valores que são fatoriais.
-
Situação 3:
- Soma de potências de dois com soma de fatoriais.
-
Situação 1: Soma somente de valores potências de dois.
- Esse é nosso limite inferior de k, podemos calcular contando quais são os bits ativos de n.
ll bits_ativos(ll n){
ll x = 0, pot = 1, k = 0;
while (n > x){
if (num & (pot)){
x += (pot);
k++;
}
pot *= 2;
}
return k;
}- Equivalente com complexidade O(numero_de_bits) :
ll bits_ativos(ll n){
return __builtin_popcountll(n);
}Builtin functions of GCC compiler
- Situação 2: Soma somente de valores que são fatoriais.
- Primeiro, precisamos saber quais são os fatoriais possíveis. No problema é descrito que n <= 10¹² , logo, precisamos apenas pré-calcular até o fatorial 14!, já que 15! = 1.307.674.368.000 > 10¹².
#define MAX_FAC 14
fac = vector<ll>(MAX_FAC + 1);
void pre_processar_fatoriais(){
ll x = 1;
for (int i = 1; i <= MAX_FAC; i++){
x *= i;
fac[i] = x;
}
}- Todos fatoriais que podem ser usados no problema:
Fatoriais (14) = {1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, 87178291200}
- Situação 2: Soma somente de valores que são fatoriais.
- Como o número de fatoriais possíveis é 14, conseguimos pré-calcular todas as somas possíveis entre esses fatoriais. Ou seja, gerar todos subsets de soma possíveis para os 14 números. O(2¹⁴ ), como 2¹⁴ = 16.384, passa tranquilo no problema.
void subset_sum_fac(ll x){
if (x == MAX_FAC+1){
ll sum = 0;
for (int i = 0; i < subset.size(); i++){
sum += fac[subset[i]];
}
if(fac_sub[sum]!=0)
fac_sub[sum] = min(fac_sub[sum],subset.size());
else
fac_sub[sum] = subset.size();
}
else{
subset.push_back(x);
subset_sum_fac(x + 1);
subset.pop_back();
subset_sum_fac(x + 1);
}
}- Situação 3: Soma de potências de dois com soma de fatoriais
- Como todas as somas de todos possíveis fatoriais podem ser salvas em um map, podemos passar por cada uma das somas que encontramos na Situação 2 e calcular um número x que diz quanto falta para a soma da Situação 2 chegar em n. Assim, conseguimos calcular para x a Situação 1.
for (map<ll, ll>:: iterator itr =
fac_sub.begin();itr!=fac_sub.end();++itr)
{
ll a = itr->first;
if (a > n) break;
ll x = n - a; //Quanto falta para a soma 'a' chegar em 'n'
minimo = min(minimo, bits_ativos(x) + fac_sub[a]);
}
Sit_1 = bits_ativos();
Sit_2 = todas_somas_possiveis_dos_fatoriais
for(i=0;i<=Sit_2.size();i++)
Sit_3 = min(Sit_3, Sit_2 [i] + Sit_1 (n - Sit_2 [i]))
k_minimo = min (Sit_1(n) , Sit_3 )E - Su Doku
-
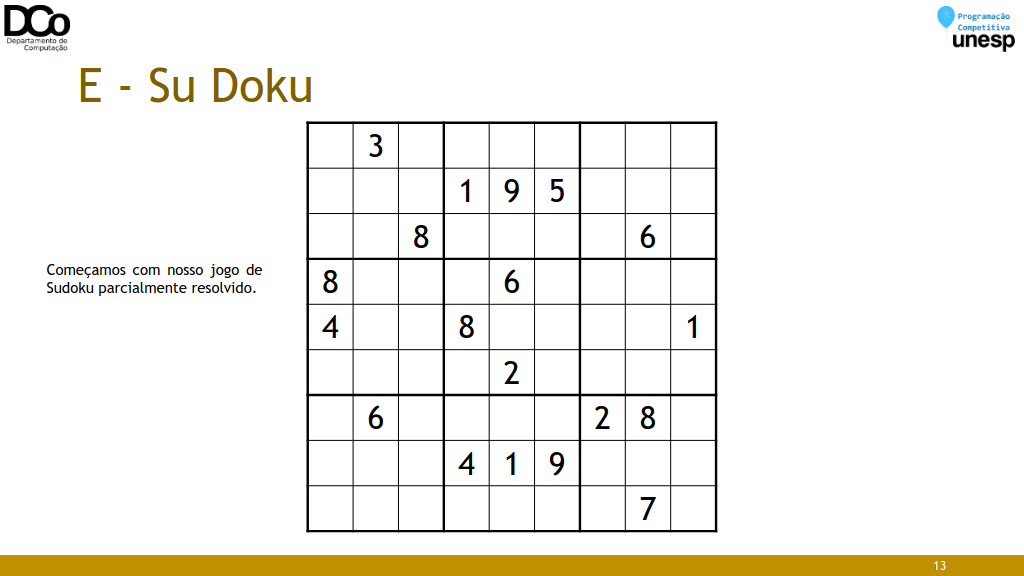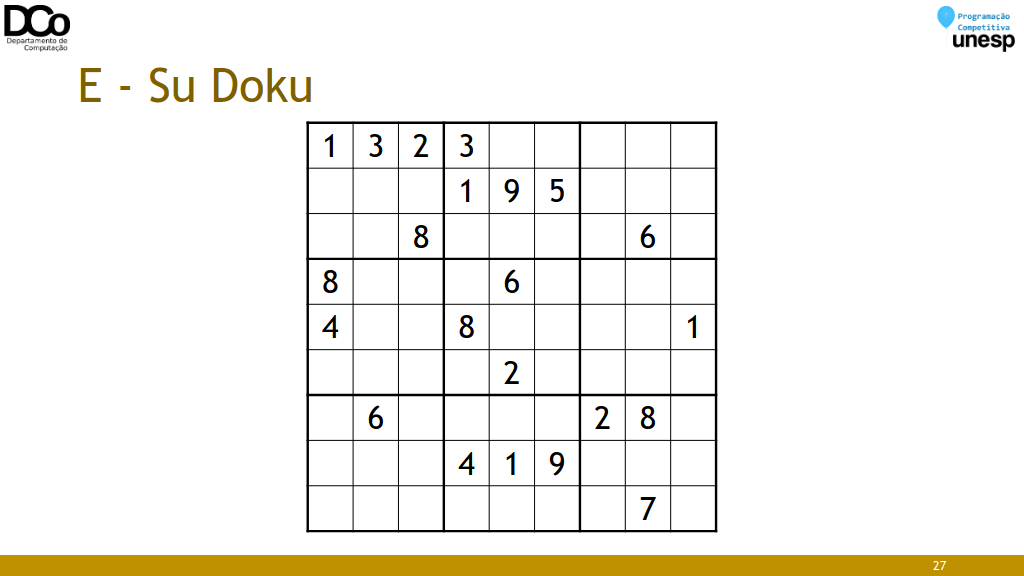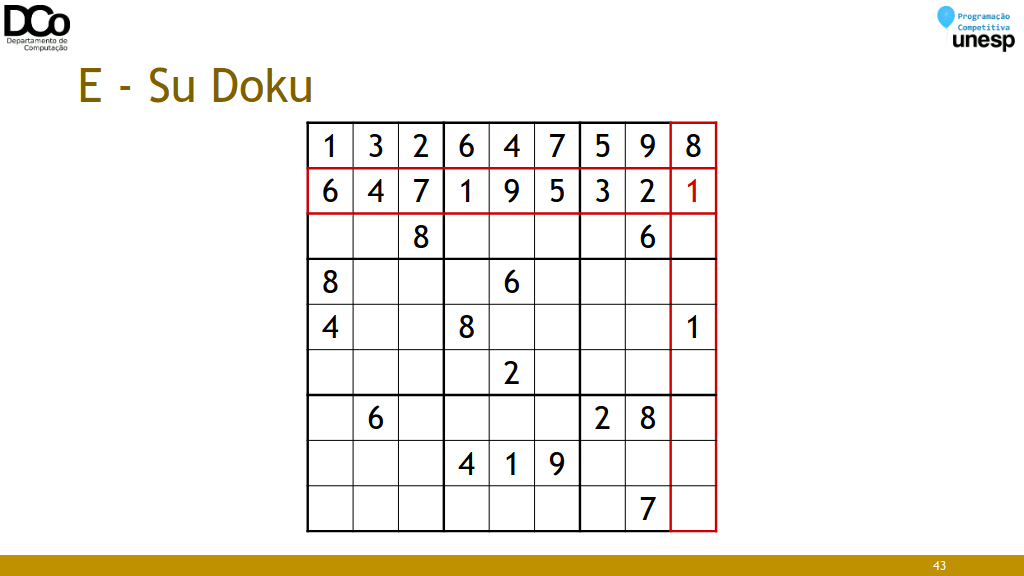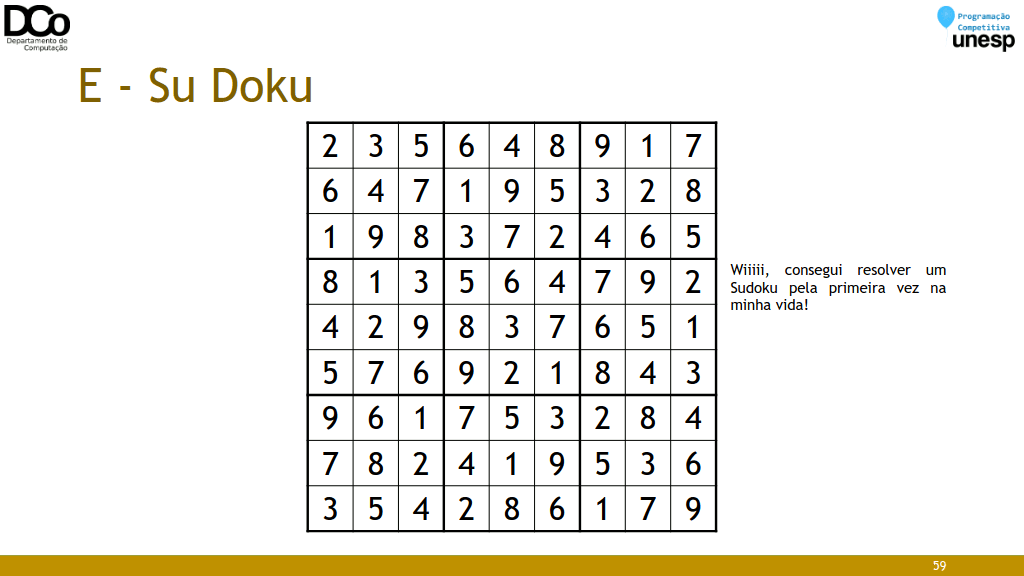
Dado um valor N e uma grade N 2 xN 2 de um Sudoku parcialmente resolvida, o objetivo é completar o quebra-cabeças, inserindo números de 1 até N 2 nas células vazias de modo que:
-
todos os números que compõem uma linha sejam distintos;
-
todos os números que compõem uma coluna sejam distintos;
-
todos os números que componham uma subgrade de tamanho NxN sejam distintos.
-
Confira na GIF abaixo:
int main() {
// leitura do tamanho do tabuleiro e alocação da matriz do Sudoku
while (cin >> n) {
n *= n;
sudoku = vector<vector<int>>(n, vector<int>(n));
// leitura do Sudoku
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> sudoku[i][j];
// se o tabuleiro apresentar solução
if (solve(0, 0)) {
// imprime a solução
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << sudoku[i][j] << " ";
cout << "\n";
}
} else
// caso contrário, imprime que não há solução viável
cout << "NO SOLUTION\n";
}
return 0;
}
bool solve(int row, int col) {
// verifica se chegou ao final da coluna atual
if (col == n) {
// se sim, pula para a linha de baixo e volta para primeira coluna
col = 0;
row++;
// caso passe da última linha, o quebra-cabeças tem solução e
// retorna verdadeiro
if (row == n)
return true;
}
// verifica se a célula atual é uma célula vazia
if (sudoku[row][col] == 0) {
// sendo uma célula vazia, vamos tentar inserir valores de 1
// até n^2 nela
for (int i = 1; i <= n; i++) {
// verificamos se é possível inserir o valor i, respeitando as
// regras do jogo
if (verify(row, col, i)) {
// em caso afirmativo, alteramos o valor da célula
sudoku[row][col] = i;
// e tentamos resolver a próxima casa
if (solve(row, col + 1))
return true;
}
}
// se nenhum valor retornar uma solução válida, esvaziamos a casa
sudoku[row][col] = 0;
} else
// se já é uma célula com valor, avançamos para a próxima
// coluna apenas
return solve(row, col + 1);
// se o código chegar até aqui, quer dizer que, para o tabuleiro no
// estado atual, não tem solução
// assim, retornamos na recursão, e tentamos achar uma solução para
// próxima configuração
return false;
}
bool verify(int row, int col, int elem) {
for (int i = 0; i < n; i++) {
// verifica se existem elementos repetidos na linha
// caso exista elemento repetido, retorna falso
if (sudoku[i][col] == elem)
return false;
// verifica se existem elementos repetidos na coluna
else if (sudoku[row][i] == elem)
return false;
}
// determina o inicio da linha e da coluna do subquadrado atual
int sq, sub_row, sub_col;
sq = sqrt(n);
sub_row = row / sq * sq;
sub_col = col / sq * sq;
// verificar se existem elementos repetidos no subquadrado
for (int i = sub_row; i < sub_row + sq; i++) {
for (int j = sub_col; j < sub_col + sq; j++) {
// caso exista elemento repetido, retorna falso
if (sudoku[i][j] == elem)
return false;
}
}
// se chegou até aqui, todas as especificações foram atendidas e retorna
// verdadeiro
return true;
}- Complexidade: O(N^M), onde N é quantidade de números possíveis de serem inseridos em cada célula do Sudoku e M a quantidade de células vazias. Ex: Sudoku resolvido, 9x9 com 63 casas vazias, teria complexidade O(9⁶³ ).