01 - Força bruta, recursão e backtracking

Paradigmas de Projeto de Algoritmos

• Determinados problemas requerem abordagens adequadas em suas resoluções;
• Dependendo da estratégia adotada, o desempenho do algoritmo pode ser ineficiente, resultando em TLE;
• Os paradigmas são como estratégias de como abordar e modelar uma solução de maneira eficiente quando aplicados corretamente.

Exemplos

• Indução Matemática
• Força Bruta
• Recursividade
• Backtracking (Tentativa e Erro)
• Algoritmos Gananciosos
• Divisão e Conquista
• Programação Dinâmica
• Algoritmos Aproximados (Heurísticas)

Força Bruta

• Algoritmos simples;
• Percorrem o espaço de busca do problema, procurando todas as possíveis soluções candidatas, verificando quais satisfazem a questão inicial;
• Varredura “cega”;
• Útil para pequenos problemas;
• Fácil implementação;
• Sempre que existir uma solução, o algoritmo irá encontrá-la.
• Exigem grande esforço computacional, seu custo tende a crescer exponencialmente.

The Closest Pair Problem

• Confira a GIF abaixo:

double euclidean(double x1, double y1, double x2, double y2) {
    return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}

int main() {
    int n;
    cin >> n;

    vector<double> x(n), y(n);

    for (int i = 0; i < n; i++)
        cin >> x[i] >> y[i];

    double mi = INF;

    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            double dist = sqrt(euclidean(x[i], y[i], x[j], y[j]));
            mi = min(mi, dist);
        }
    }

    cout << dist << "\n";

    return 0
}

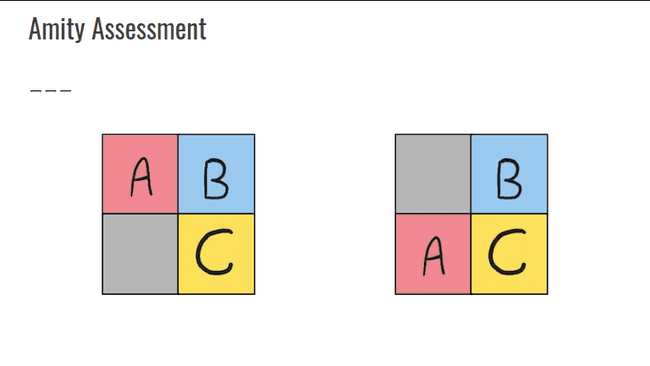
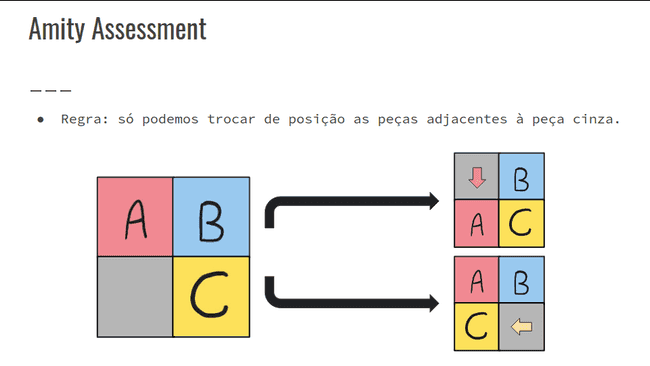
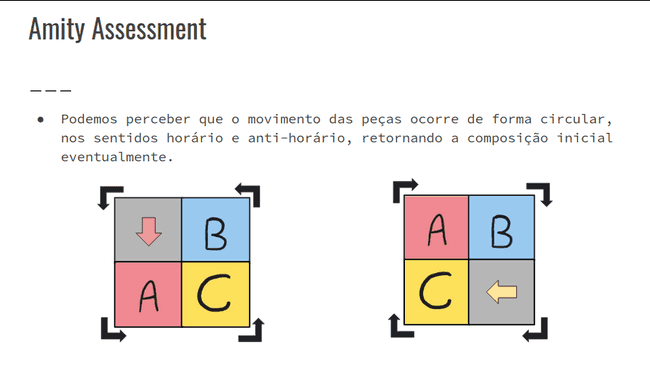
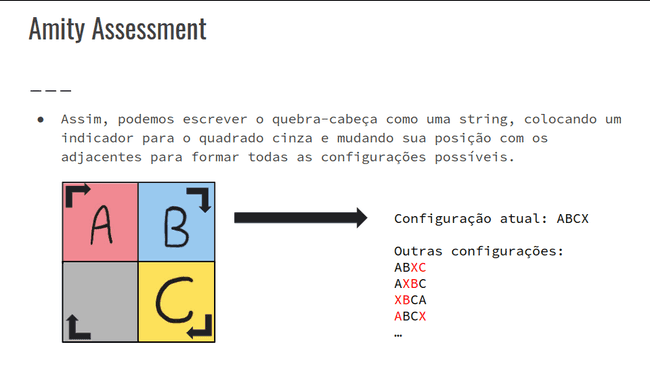
Amity Assessment

Sugestão de Problemas

• The Closest Pair Problem - UVa
• Amity Assessment - Codeforces

Recursividade

• Mecanismo no qual a definição de uma função ou de um objeto se refere ao próprio objeto definido;
• Permite descrever problemas que utilizam estruturas recursivas de forma clara e concisa;
• Um procedimento que opera em termos de si mesmo é dito ser recursivo.

Gerando Subconjuntos

• Nossa primeira aplicação da recursão será gerar todos os subconjuntos de um conjunto de N elementos;

Gerando Permutações

• A segunda aplicação de recursão que veremos será gerar todas as permutações de um conjunto de N elementos;

Desafio

• Amity Assessment - Codeforces
  • Generalizar a solução do problema para 2 ≤ N ≤ 10, elencando todas as possíveis soluções do quebra-cabeças com um algoritmo recursivo.

Backtracking

• Aperfeiçoamento do algoritmo de força bruta;
• Várias soluções da força bruta são eliminadas, visto que não são testadas;
• Inicialmente se tem uma solução vazia e vamos estendendo ela passo apasso, incrementalmente.

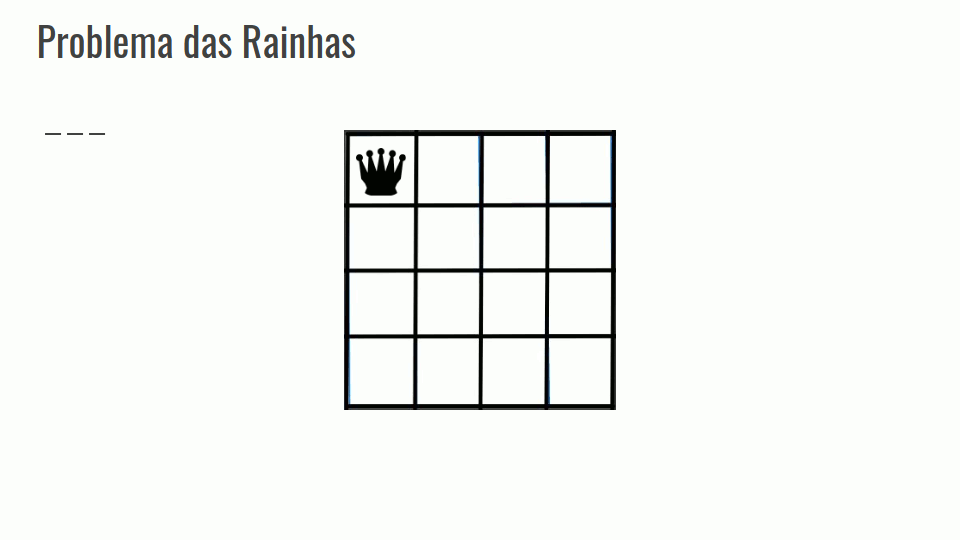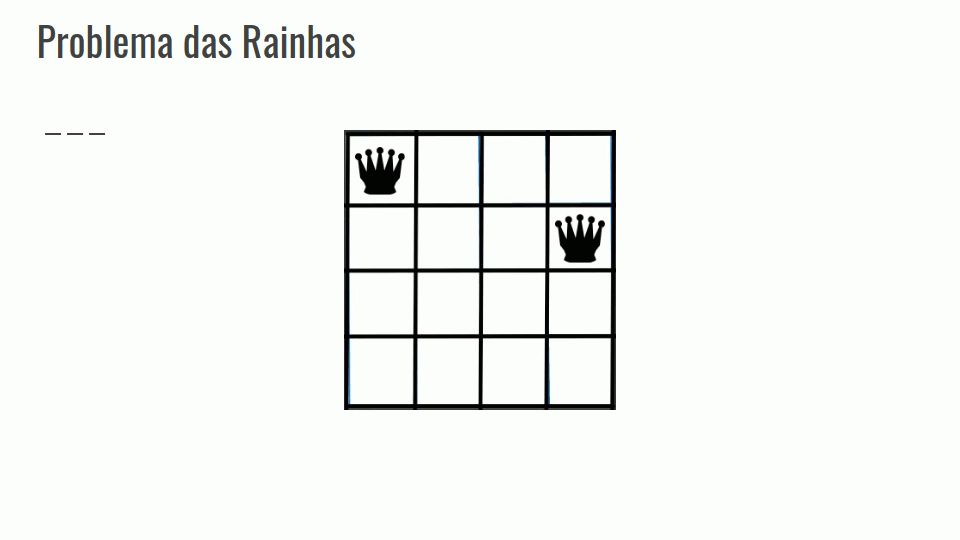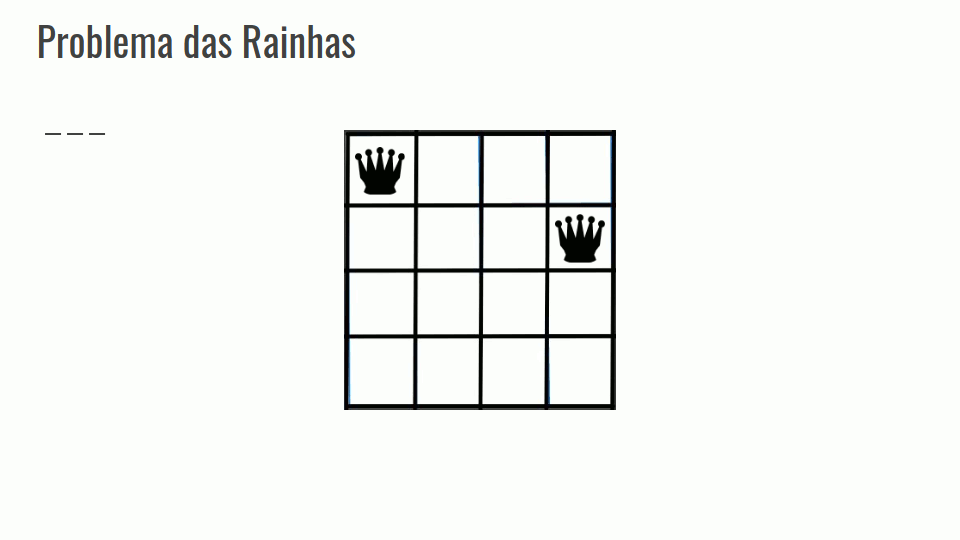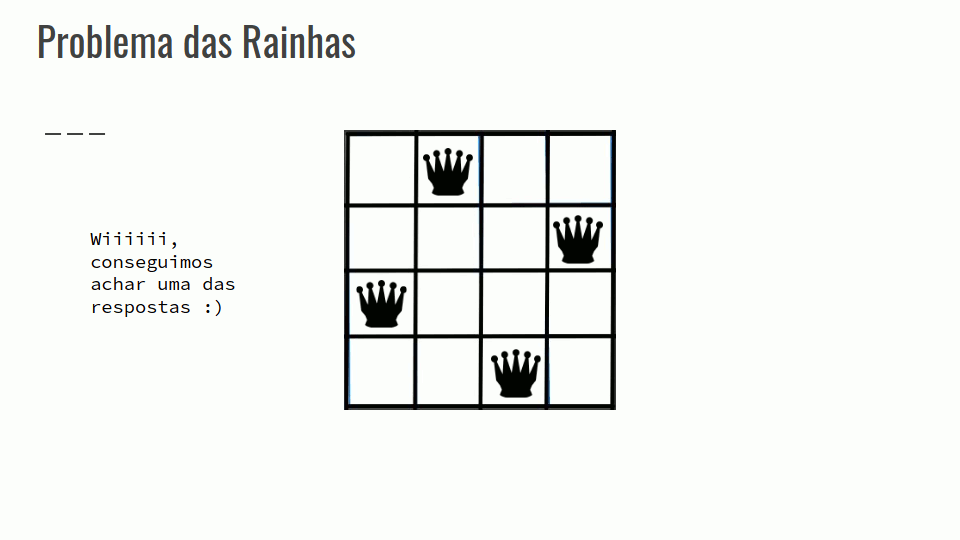
Problema das Rainhas

• Calcular o número de maneiras de se colocar N rainhas em um tabuleiro NxN.

• Em um problema de backtracking inicia-se com uma solução vazia, nesse caso com o tabuleiro vazio.

• A partir do tabuleiro vazio a solução é estendida passo a passo até que se consiga colocar todas as N rainhas.

• Confira a GIF abaixo:

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

vector<bool> diagonal, diagonal2, coluna, linha;

ll n;

ll cont = 0;

void colocar_rainha(ll lin, ll col) {
    if (lin == n+1) {
        cont++;
        return;
    }
    
    if (col == n+1) return;

    if (diagonal[n + (lin - col)] || diagonal2[lin+col] 
        || coluna[col] || linha[lin]) {
        colocar_rainha(lin, col+1);
    }

    else {
        colocar_rainha(lin+1, 0);
    }

    return;
}

Sugestão de Problemas

• Chessboard and Queens - CSES
• MKJUMPS - SPOJ

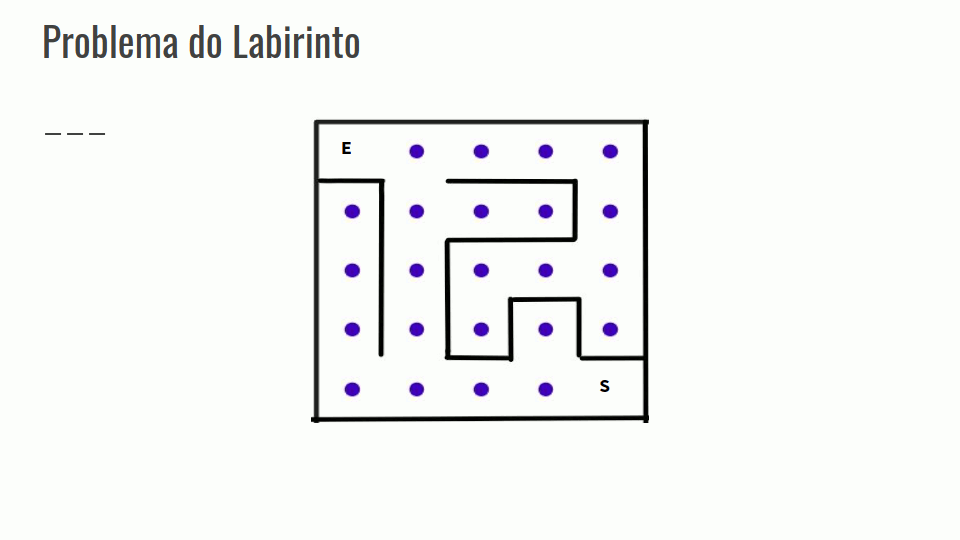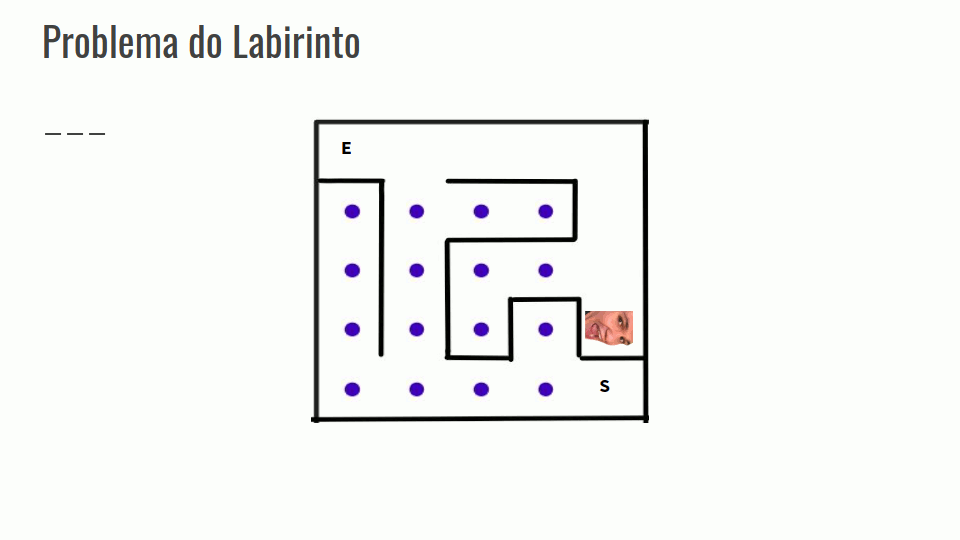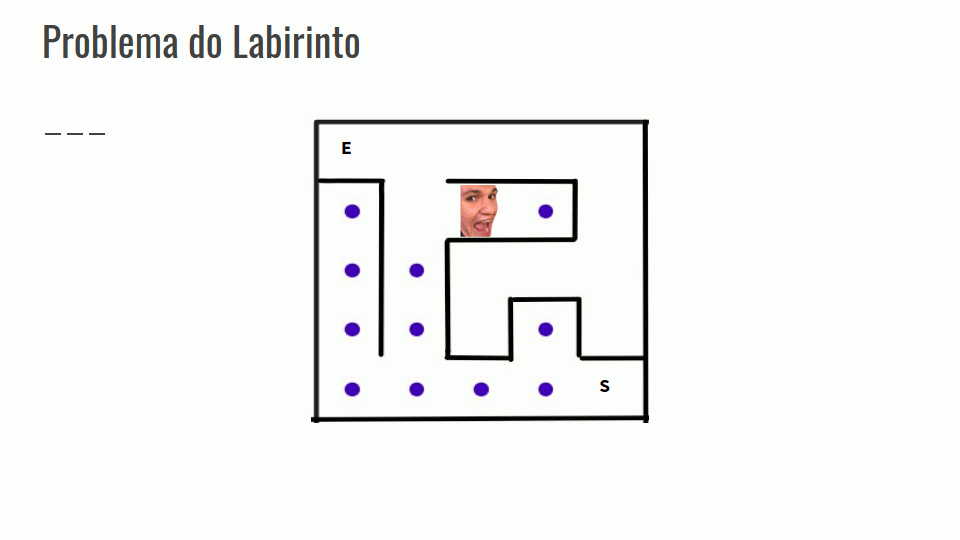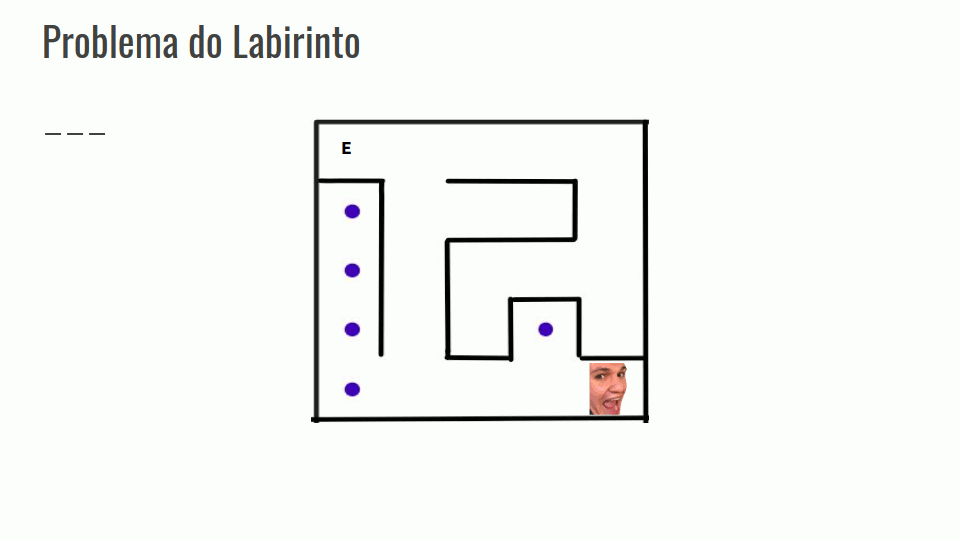
Problema do Labirinto

• Encontrar um caminho da entrada do labirinto até a saída.
• Gerar a solução por partes, e quando encontrarmos em um beco sem saída, retornar os passos até que se possa ter acesso à outro caminho.
• Confira na GIF abaixo:

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

vector<pair<ll,ll>> mov = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
vector<vector<bool>> vis;
ll linha_final = 5, coluna_final = 5;

bool flag = false;

void andar(ll lin, ll col) {
    if (flag) return;

    if (lin == linha_final && col == coluna_final) {
        flag = true;
        return;
    }

    if (vis[lin][col]) return;
    vis[lin][col] = true;

    for (int i = 0; i < mov.size(); i++) {
        ll nova_linha, nova_coluna;
        nova_linha = lin + mov[i].first;
        nova_coluna = col + mov[i].second;
        andar(nova_linha, nova_colunar);
    }

    return;
}

Sugestão de Problemas

• Grid Paths - CSES - Difícil
• Labyrinth - CSES

Problema do Sudoku

• Problema: dado um Sudoku parcialmente resolvido, determinar se existe solução para aquele problema;
• Vídeo de explicação do problema do Sudoku