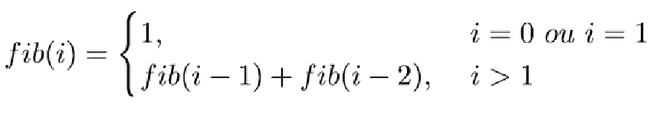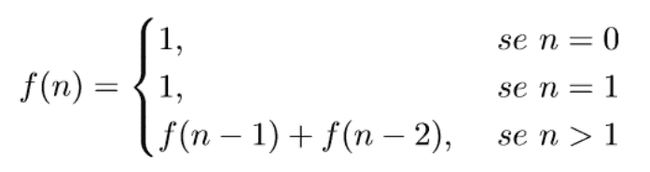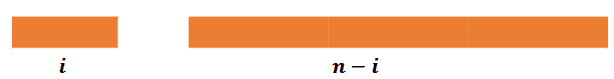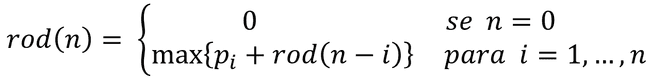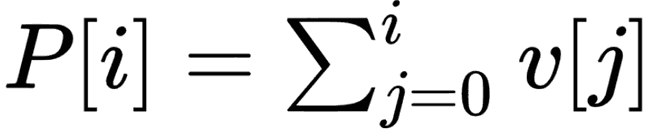01 - Programação Dinâmica Parte I

Algoritmos com 'memória'

Autor(es): Rene Pegoraro, Pedro Henrique Paiola, Wilson M Yonezawa

Origem

Introduzido por Richard Bellman da década de 50, em um projeto militar na RAND Corporation.
O termo foi utilizado para encobrir o propósito do projeto, pois o Secretário de Defesa da época abominava pesquisa matemática.

"A década de 1950 não foi boa para a pesquisa em matemática. Tivemos um cavalheiro muito interessante em Washington chamado Wilson. Ele foi secretário de Defesa, e realmente tinha um medo patológico e ódio da palavra 'pesquisa'. Não estou usando o termo levemente; eu estou usando-o precisamente. Seu rosto ficava vermelho, e ele ficava violento se as pessoas usassem o termo 'pesquisa' em sua presença. Você pode imaginar como ele se sentia então, sobre o termo 'matemática'." (Richard Bellman)

Programação Dinâmica

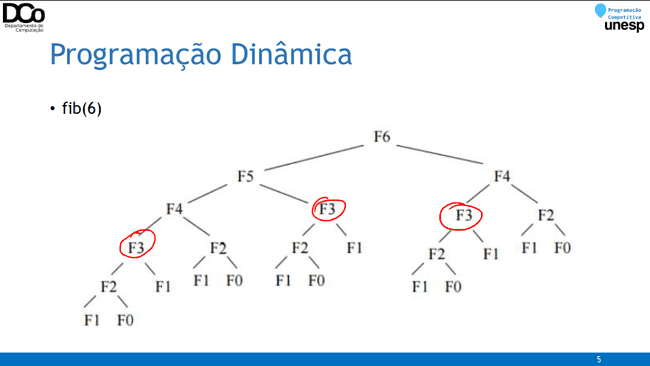
Tomemos como exemplo um algoritmo recursivo para solucionar o problema de encontrar o i-ésimo termo da sequência de Fibonacci.

int fib(int i) {
    if (i == 0 || i == 1)
        return 1;
    return fib(i-1) + fib(i-2);
}

“Quem não se lembra do passado é condenado a repeti-lo”
Em algoritmos que usam a estratégia da divisão e conquista é comum haver a repetição de subproblemas (overlapping subproblems), como exemplificado no algoritmo para calcular termos da sequência de Fibonacci.
Isso pode acabar gerando muito recálculo.
A PD vem para tentar resolver este problema.
A ideia básica da Programação Dinâmica é armazenar a solução dos subproblemas para serem utilizados no futuro.
Isso pode ser feito por duas abordagens:
Top Down (Memoization)
Bottom Up (Tabulation)
É importante ressaltar: para que esse paradigma possa ser aplicado, é preciso que o problema tenha uma estrutura recursiva, a solução de toda instância do problema deve “conter” soluções de subinstâncias dessa instância.

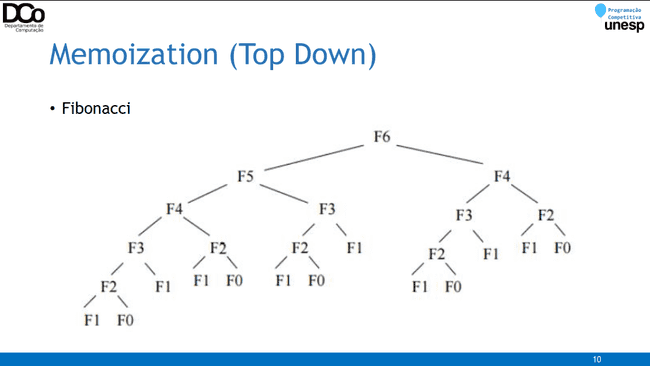
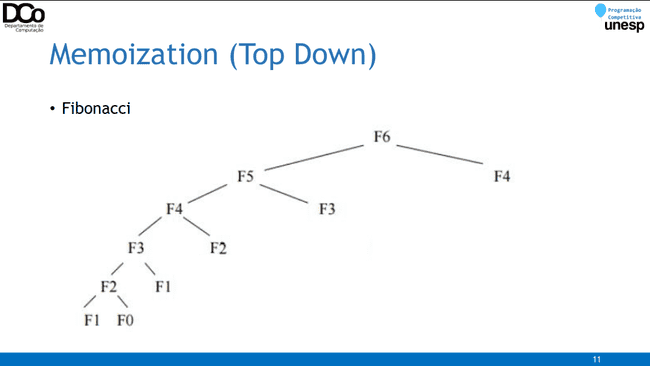
Memoization (Top Down)

Do geral para o específico, de cima para baixo.
Normalmente essa abordagem é a mais simples de se aplicar, pois ainda faz o uso de algoritmos recursivos.
Visita apenas os estados requisitados.
Método:
- O problema é dividido em subproblemas.
- Cada subproblema é resolvido recursivamente.
- Quando um subproblema é resolvido, o resultado é armazenado para possíveis utilizações no futuro (memoization).
Fibonacci:

int memo[] = {1, 1, -1, -1, -1, -1, …} //-1 = não calculado
int fib(int i){
    if (memo[i] == -1)
        memo[i] = fib(i-1) + fib(i-2);
    return memo[i];
}

Tabulation (Bottom Up)

Do específico para o geral, de baixo para cima.
Visita todos os estados.
Método:
- O problema é dividido em subproblemas.
- Cada subproblema é resolvido, se iniciando pelos que são base para a solução dos seguintes (de forma geral, isso é feito iterativamente).
- Quando um subproblema é resolvido, o resultado é armazenado para resolver subproblemas futuros, até alcançar o problema original.
Fibonacci

int memo[MAXN];
void preprocess(int n){
    memo[0] = memo[1] = 1;
    for(int i = 2; i < n; i++)
        memo[i] = memo[i-1] + memo[i-2];
}
int fib(int i){
    return memo[i];
}

Propriedades necessárias

Subestrutura ótima:
A solução ótima do problema é composta pela solução ótima de partes menores e mais simples do problema.
Exemplo:

fib(n) = fib(n-1) + fib(n-2)

Lembrando que, nem sempre é fácil ou intuitivo ver como as soluções dos subproblemas devem ser combinadas para obter a solução do problema original.
Exemplo: par de pontos de menor distância
Sobreposição de subproblemas:
- É necessário haver a repetição de subproblemas, do contrário, não faz muito sentido armazenar a solução de um subproblema que nunca mais será necessária
- Exemplos:
- fib(5) = fib(4) + fib(3)
- fib(4) = fib(3) + fib(2)
- ...
- fib(3) = fib(2) + fib(1)
- ...
O problema do par de pontos mais próximos, apesar de apresentar subestrutura ótima, não apresenta sobreposição de subproblemas.

PD x Outros paradigmas

Algoritmo Guloso
- Melhor solução local
Backtracking
- Busca exaustiva
- Complexidade fatorial/exponencial
Programação Dinâmica
- Melhor solução global/solução ótima
- Busca exaustiva “inteligente”
- Evita recalcular problemas que já ocorreram
- Complexidade polinomial

Estratégia geral

A ideia básica da Programação Dinâmica é simples, o desafio é aplicar isso em diferentes problemas.
Não existe uma “receita de bolo” para fazer isso, mas existem dicas e estratégias.
Em especial, temos que nos focam em encontrar padrões de recorrência no nosso problema
Usos convencionais:
Encontrar uma solução ótima
Contar o número de soluções possíveis

Definir os subproblemas
Escrever a recorrência que relaciona os subproblemas
Reconhecer e solucionar os casos base

Aplicando à Sequência de Fibonacci

Definir os subproblemas

fib(i) -> subproblemas: fib(i-1) e fib(i-2)

Escrever a recorrência que relaciona os subproblemas

fib(i) = fib(i-1) + fib(i-2)

Reconhecer e solucionar os casos base

fib(0) = 1 e fib(1) = 1

Dicas do Thiago Alexandre de como estudar programação dinâmica:
Decorar algoritmos não adianta, entenda a lógica e as diferentes técnicas;
Estudar, entender e treinar problemas recursivos;
Estudar, entender e treinar problemas clássicos de PD;
Resolva problemas e compare com outras soluções;
O que outras soluções têm de melhor ou pior?

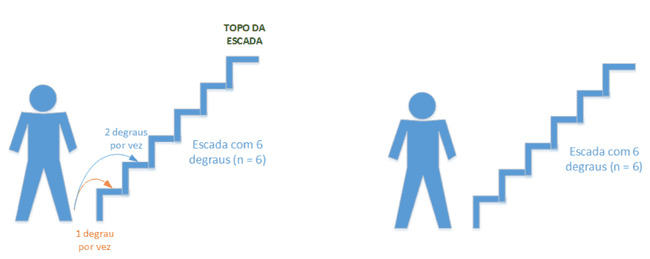
Problema da Escada

Quantas formas há de subir uma escada de n degraus, sendo que em cada passo pode-se subir 1 ou 2 degraus por vez?

Quantas formas há de subir uma escada de n degraus, sendo que em cada passo pode-se subir 1 ou 2 degraus por vez?
Exemplos de possibilidades para n = 6:

1, 1, 1, 1, 1, 1

2, 1, 1, 1, 1

2, 2, 2

2, 1, 1, 2

1, 1, 1, 1, 2

Vamos considerar que nosso problema será resolvido por uma função 𝒇(𝒏), onde 𝒏 é o número de degraus.
Considerando que já estamos no degrau 𝒏, em quais degraus poderíamos estar no passo anterior?
𝑛 − 1
𝑛 − 2
Dessa forma, o número de possibilidades de chegar no degrau 𝒏 é a soma do número de possibilidade de chegar no degrau 𝒏 − 𝟏 com o número de possibilidades de chegar no degrau

𝒏 − 𝟐.

Problema do Troco

Problema: dar troco de um valor x com o menor número de moedas possíveis.
Já vimos a solução utilizando backtracking e algoritmo guloso.
Embora a solução gulosa seja bastante eficiente, ela nem sempre leva a uma solução ótima (dependendo das moedas disponíveis)
A solução por PD irá se basear na solução por backtracking, mas memorizando as respostas para lidar com a sobreposição de subproblemas.
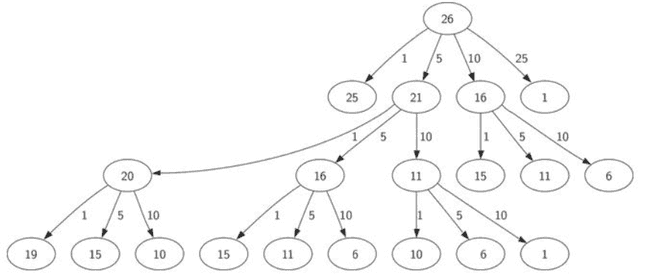
Para moedas = {1, 5, 10, 25} e troco = 26 temos a seguinte árvore de recursão:

Relação de recorrência

Implementação (Top-down):

int troco(int x){
    if (x == 0)
        return 0;
    if (memo.count(x))
        return memo[x];
    memo[x] = INT_MAX;
    for(int m : moedas){
        if (m > x)
            continue;
        memo[x] = min(memo[x], 1 + troco(x-m));
    }
    return memo[x];
}

Implementação (Bottom-up):

// Complexidade de tempo: O(N*W)
int minCoins(vector<int>& moedas, int w) {
    int n = moedas.size();
    vector<int> dp(w+1, INT_MAX);
    dp[0] = 0;
    for (int i = 1; i <= w; i++)
        for (int j = 0; j < n; j++)
            if (moedas[j] <= i)
                dp[i] = min(dp[i], dp[i-moedas[j]]+1);
    return dp[w];
}

Corte do bastão (rod cutting)

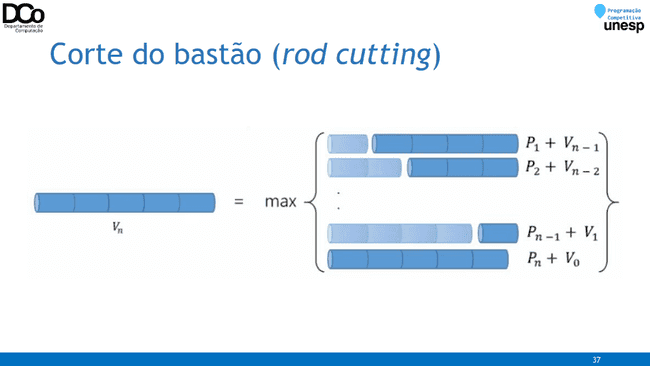
Dado um bastão de madeira de comprimento 𝑛 e uma tabela p de preços (venda) de cortes de 𝑛.
Objetivo: determinar o valor máximo obtido cortando o bastão e vendendo os pedaços (cortes) ou o bastão inteiro

Tamanho (cortes)	Preço
1	R$ 1,00
2	R$ 5,00
3	R$ 8,00
4	R$ 9,00

Tentando encontrar a recorrência do problema:
Nosso objetivo é maximizar o valor obtido de um bastão de tamanho 𝒏, vamos considerar que isso seja o resultado da função 𝒓𝒐𝒅(𝒏)
Se fizermos um corte de tamanho 𝒊 nesse bastão, vamos obter um bastão de tamanho 𝒊 e um novo bastão de tamanho 𝒏 − 𝒊

Vamos considerar que não podemos mais fazer cortes no bastão de tamanho 𝒊, apenas no bastão de tamanho 𝒏 − 𝒊.
Nesse caso, a solução seria p[i] + rod(n - i)
A base da nossa solução será fazer isso para todos os possíveis cortes 𝒊, então podemos generalizar o problema da seguinte forma:

int rodCutter(int p[], int n){
    int rod[n+1];
    rod[0] = 0;
    for(int i = 1; i <= n; i++){
        int max_val = -INF;
        for(int j = 1; j <= i; j++)
            max_val = max( max_val, p[j] + rod[i-j] );
        rod[i] = max_val;
    }
    return rod[n];
}

Prefix Sum

Uma possibilidade é utilizar um vetor de soma de prefixos.
Basicamente, uma posição i desse vetor armazena a soma de todos os valores entre 0 e i.

Com essas informações, podemos responder uma consulta (l,r) muito facilmente, como veremos a seguir:
Dados o vetor v e seu vetor de soma de prefixos P subjacente:
Confira na GIF abaixo:

img15-img18

Assim, podemos generalizar uma consulta q como sendo:
- 𝑞(𝑙, 𝑟) = 𝑃[𝑟] − 𝑃[𝑙 − 1]
Por este método, temos as seguintes complexidades:
- Alteração: 𝑂(𝑛)
- Consulta: 𝑂(1)
Esta é uma ED muito interessante para quando não há (ou há poucas) atualizações nos valores do vetor.

Prefix Sum - Aplicações

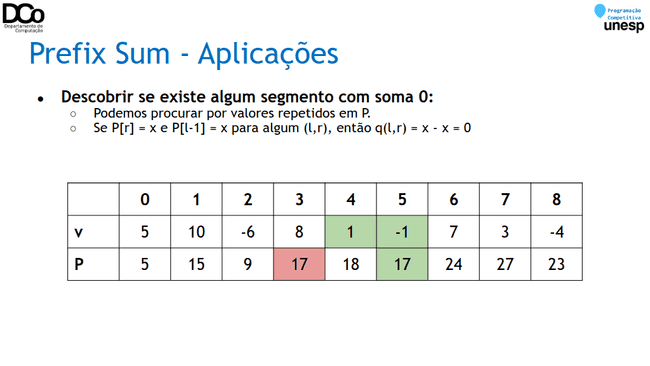
Encontrar o índice de equilíbrio:
- Encontrar o índice i para qual: v[0...i-1] = v[i+1...n-1]
- Solução: buscar i para qual vale que P[i-1] == P[n-1] - P[i]

Sugestões

Seminário sobre Programação Dinâmica da equipe UnespRPM: https://youtu.be/xYDOE8hG7Uk

DP Tutorial and Problem List: https://codeforces.com/blog/entry/67679

Referências

Rene Pegoraro. Aulas de Técnicas de Programação.

Rene Pegoraro e Wilson M. Yonezawa. Aulas de Algoritmos Avançados.

Thiago Alexandre Domingues de Souza. Palestra sobre Programação Dinâmica.

Giulia Moura, João Pedro Comini e Pedro H. Paiola. Aulas de Programação Competitiva I.

Bruno Papa, Maurício Scarelli e Rodrigo Rosseti. Seminário sobre Programação Dinâmica.

LAAKSONEN, A. Competitive Programmer’s Handbook.

https://www.ime.usp.br/~pf/analise_de_algoritmos/aulas/dynamic-programming.html

http://www.decom.ufop.br/anderson/2_2012/BCC241/ProgramacaoDinamica.pdf

https://www.geeksforgeeks.org/tabulation-vs-memoizatation/

https://www.geeksforgeeks.org/solve-dynamic-programming-problem/

https://github.com/UnBalloon/programacao-competitiva/tree/master/Preffix%20sums%20(Somas%20de%20prefixos)