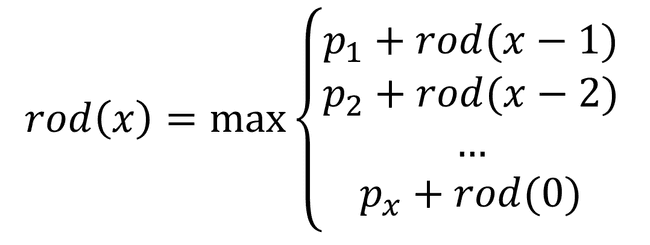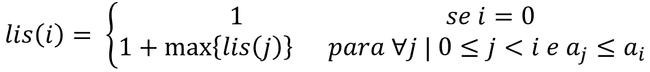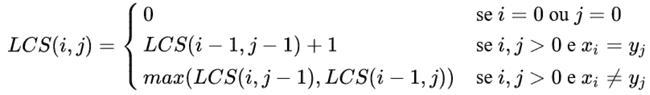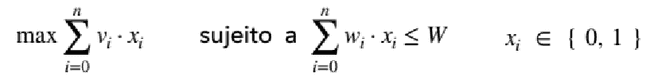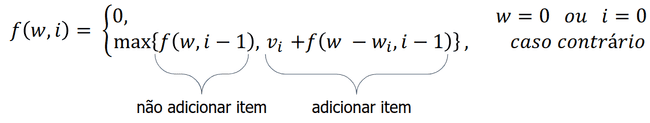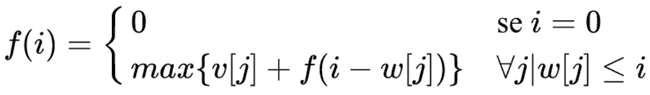02 - Programação Dinâmica Parte II
Continuação
Autor(es): Pedro Henrique Paiola, Rene Pegoraro, Wilson M Yonezawa, Arissa Yoshida, Nicolas Barbosa Gomes, Luis Henrique Morelli
Revisando
-
Algoritmos com estrutura recursiva, divisão e conquista
-
Ideia: armazenar a solução de subproblemas para a resolução de problemas futuros
-
Ideia é simples, o desafio é aplicar isso em diferentes problemas.
-
Estratégias e dicas
-
Ou, de forma análoga, podemos considerar os seguintes passos para resolver um problema de PD:
- Identificar se é um problema de PD
- Definir os estados do problema
- Definir a relação entre os estados
- Implementar a solução usando tabulation ou memoization
Identificando o problema
- Na aula passada trabalhamos este passo com mais detalhes.
- Para podermos aplicar PD, o problema deve ter uma estrutura recursiva e apresentar as seguintes propriedades:
- Subestrutura ótima
- Sobreposição de subproblemas
- Problemas típicos:
- Encontrar a solução ótima de um problema, que maximize ou minimize um determinado valor.
- Contar o número de soluções possíveis.
Definir os estados do problema
- Problemas de PD podem ser caracterizados por estados e transições
- Corte do bastão
- Estado: bastões resultantes dos cortes
- Transição: novo corte
- Troco
- Estado: moedas utilizadas até o momento e valor que falta a ser trocado
- Transição: adição de uma nova moeda
- A representação dos estados do problema devem ser feitos com um certo cuidado, pois isso vai afetar diretamente a próxima etapa, de definir a relação entre os estados, as transições
- Estado: um estado pode ser definido como um conjunto de parâmetros que identifica, unicamente, uma posição ou “situação” de um dado problema.
- Esse conjunto de parâmetros deve ser o menor possível, especialmente para reduzir o espaço necessário para armazenar as soluções dos subproblemas.
- Exemplos:
- Fibonacci: i (i-ésimo termo)
- Troco: valor a ser trocado
- Bastões: tamanho do bastão ou pedaço a ser cortado
- Se o estado que define uma certa instância (ou subinstância) do seu problema apresenta muitos parâmetros, sua solução deve ser ineficiente.
- A solução pode também ser ineficiente em relação ao tempo, mas principalmente em relação ao espaço, demandando muita memória para armazenar as soluções de subproblemas.
- Definir o melhor estado possível para as instâncias do problema é um passo primordial da aplicação de PD.
- Atente-se a parâmetros redundantes ou inúteis.
Definir a relação entre os estados
-
Provavelmente a parte mais difícil na resolução de um problema de PD.
-
Dependendo do problema, requer bastante intuição, observação e prática.
-
Como ocorrem as transições entre estados? Quais são as decisões possíveis?
-
Como definir a solução de um problema em função dos seus subproblemas?
-
Encare o problema como sendo um problema de decisão: a partir de um certo estado, há um conjunto de decisões (ações, transições) possíveis, e deve-se determinar qual decisão leva a solução ótima.
-
Cada transição leva a um determinado estado. Supondo que se conhece a solução de todos os estados para quais podemos avançar, como posso combinar essas informações para obter a solução do estado atual?
-
Problema do troco:
- Estado: valor a ser trocado
- Decisões possíveis: moedas disponíveis
- Para cada moeda adicionada, temos um novo valor a ser trocado. Como estamos adicionando apenas uma moeda, a melhor decisão é aquela que leva ao valor que precisa do menor número de moedas para ser trocado.
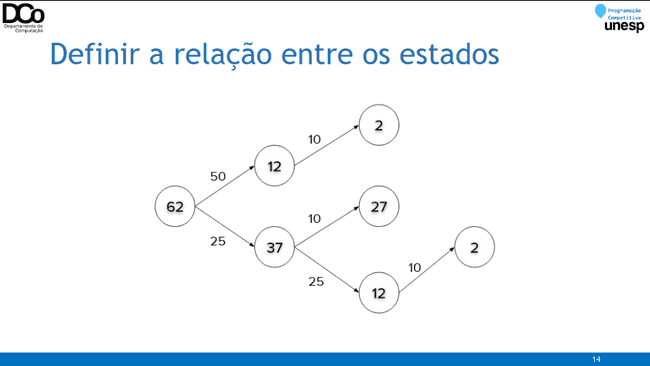
- Problema do corte do bastão:
- Estado: tamanho do bastão
- Decisões possíveis: cortes
- Vamos considerar que em cada passo realizamos apenas um corte. A melhor decisão é o corte obtém o maior valor total, ou seja, considerando o preço do corte atual, com o maior valor possível de ser obtido com o bastão que sobrou.
- Em alguns casos, tentar elaborar um diagrama de como o problema se comporta, buscando estabelecer relações entre os estados, pode ajudar a obter insights de como solucionar o problema.
Aplicar tabulation ou memoization
- Realizar a implementação da solução em si, considerando as abordagens apresentadas na aula anterior: Top Down e Bottom Up.
- As soluções dos subproblemas devem ser armazenadas de alguma forma, no caso mais geral temos:
memo[estado] = solução do estadoMaior subsequência crescente (LIS)
- Subsequência: uma subsequência de uma sequência de elementos 𝑿 é uma sequência 𝑿’ com zero ou mais elementos de 𝑿 removidos.
- É uma sequência de elementos de 𝑿 não necessariamente contíguos.
- Exemplo:
𝑋 = {𝑨, 𝐵, 𝑪, 𝐵, 𝑫, 𝑪, 𝐵}
𝑋’ = {𝐴, 𝐶, 𝐷, 𝐶}
Maior subsequência crescente (LIS)
- Maior subsequência crescente: dado uma sequência de números, determinar a maior subsequência de valores crescentes.
Maior subsequência crescente (LIS)
- Inicialmente, vamos tentar verificar se este é um problema de PD, definindo a relação de recorrência mais intuitiva possível, sem nos preocupar com a eficiência da solução ainda.
- Se pensarmos um pouco, não é tão difícil perceber que a subsequência máxima de um vetor 𝑣[0 … 𝑛 − 1] pode ser definida a partir das subsequências máximas dos vetores 𝑣[0 … 𝑛 − 2] , 𝑣[0 … 𝑛 − 3] , ... .
- Confira a GIF abaixo:

- Agora que já sabemos que podemos aplicar PD neste problema, vamos utilizar a estratégia apresentada anteriormente para modelá-los da melhor forma possível, visando uma implementação eficiente.
- Definição dos estados
- No passo anterior, concluímos que podemos determinar a subsequência máxima do vetor 𝒗[𝟎 … 𝒏 − 𝟏] a partir das subsequências máximas dos vetores 𝒗[𝟎 … 𝒏 − 𝟐], 𝒗[𝟎 … 𝒏 − 𝟑] ...
- A partir disso, parece interessante definir o estado do nosso problema como o índice em que acaba nosso vetor.
- Subsequência máxima que TERMINA na posição i; lis(i)
- Subsequência máxima do vetor inteiro: max(lis(i)), 0 <= i < n
Relação entre os estados
- Agora temos que definir/encontrar uma relação de recorrência.
- Problema base: lis(0) , nesse caso estamos considerando apenas o primeiro elemento do vetor, obviamente a maior subsequência crescente possível é 1 (considerando o único elemento possível)
- lis(0) = 𝟏
- E o passo da recursão?
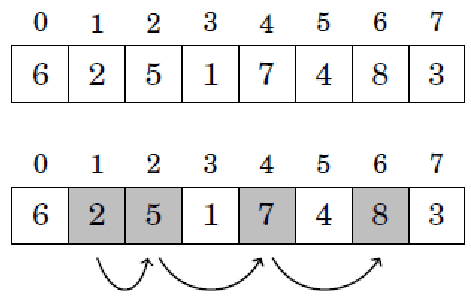
- Para lis(i) queremos encontrar a subsequência máxima que termina e contém a posição i.
- Para isso, vamos considerar as posições i | i < i
- Se a[𝒋] > a[𝒊], não vamos considerar a lis(i), pois o elemento a[𝒊] não pode ser inserida nela.
- Se a[𝒋] <= a[𝒊], então a[𝒊] pode ser inserido na lis(i), gerando uma subsequência de tamanho lis(i + 1).
- Implementação (Top-down):
memo[] = {1, -1, -1, -1, …}
int lis(int i){ //retorna a LIS que termina em a[i]
if (memo[i] != -1)
return memo[i];
memo[i] = 1;
for(int j = 0; j < i; j++)
if (a[j] <= a[i])
memo[i] = max(memo[i], lis(j) + 1);
return memo[i];
}- Implementação (Bottom-up):
int lis(int n){
int memo[n], lisMax = 0;
for(int i = 0; i < n; i++){
memo[i] = 1;
for(int j = 0; j < i; j++){
if (a[j] <= a[i])
memo[i] = max(memo[i], memo[j] + 1);
}
lisMax = max(lisMax, memo[i]);
}
return lisMax;
}- Esta solução do problema tem complexidade O(n²).
- Por força bruta, teríamos complexidade exponencial (testando todas as possíveis subsequências)
- Existem outras possíveis soluções, utilizando Programação Dinâmica e Busca Binária ou alguma estrutura de dados que trabalhe com range queries. Estas soluções atingem complexidade O (nlog(n)).
- Para mais detalhes:
https://cp-algorithms.com/sequences/longest_increasing_subsequence.html
Maior subsequência comum (LCS)
- Problema: dadas as sequências 𝑋[0. . 𝑚 − 1] e 𝑌[0. . 𝑛 − 1], encontrar uma sequência 𝑍 tal que 𝑍 é subsequência de 𝑋 e de 𝑌 e tem comprimento máximo.
- Exemplo:
𝑋 = {𝐴, 𝑩, 𝑪, 𝑩, 𝐷, 𝑨, 𝐵} 𝑌 = {𝑩, 𝐷, 𝑪, 𝐴, 𝑩, 𝑨} 𝑍 = 𝐿𝐶𝑆(𝑋, 𝑌) = {𝐵, 𝐶, 𝐵, 𝐴}
- Força bruta: testar todas as subsequências se 𝑋 para ver se ela também é uma subsequência de 𝑌.
- Há 2𝑚 subsequências de 𝑋 para serem verificadas
- Cada subsequência gasta tempo 𝑂(𝑛) para ser verificada.
- Complexidade total: 𝑂(𝑛. 2𝑚)
- Como dito anteriormente, uma subsequência de 𝑋 é uma sequência 𝑋’ com zero ou mais elementos de 𝑋 removidos.
- Pensando nisso, nosso objetivo pode ser visto como minimizar o número de elementos removidos de duas sequências para que elas se tornem iguais (ou, de forma equivalente, maximizar o número de elementos inseridos).
- Teorema: Seja 𝑍[1. . 𝑘] uma LCS de 𝑋[1. . 𝑚] e 𝑌[1. . 𝑛]
- Se 𝑥𝑚 = 𝑦𝑛 então 𝑧𝑘 = 𝑦𝑛 = 𝑥𝑚 e 𝑍[1. . 𝑘 − 1] é uma LCS de 𝑋[1. . 𝑚 − 1] e 𝑌[1. . 𝑛 − 1]
- Se 𝑥𝑚 ≠ 𝑦𝑛 então 𝑧𝑘 ≠ 𝑥𝑚, sendo assim 𝑍[1. . 𝑘] é uma LCS de 𝑋[1. . 𝑚 − 1] e 𝑌[1. . 𝑛]
- Se 𝑥𝑚 ≠ 𝑦𝑛 então 𝑧𝑘 ≠ 𝑦𝑛, sendo assim 𝑍[1. . 𝑘] é uma LCS de 𝑋[1. . 𝑚] e 𝑌[1. . 𝑛 − 1]
- Esse teorema mostra que este problema atende a propriedade da Subestrutura Ótima.
- Confira a GIF abaixo:

Problema da Mochila
- Problema:
- Uma mochila suporta até 𝑊 quilos
- Itens devem ser adicionados à mochila
- Cada item tem um peso 𝑤𝑖 e um valor 𝑣𝑖
- 𝑤𝑖 e 𝑣𝑖 são inteiros
- Objetivo:
- Qual o valor máximo que não ultrapassa o limite da mochila?
- Caso base:
- Se a capacidade da mochila ou a quantidade de itens for zero, então o valor máximo é zero.
- Passo da recursão
- Senão, há duas opções: incluir ou não incluir (considerando o problema da mochila binária, onde não há repetições de itens)
- Queremos maximizar o valor total carregado sem ultrapassar a capacidade da mochila.
w = capacidade disponível, i = item atual
- Confira a GIF abaixo:

Problema da Mochila – Top Down
int knapsack(int w, int n){
if(memo[w][n] != -1)
return memo[w][n];
if(w == 0 || n == 0)
return memo[w][n] = 0;
if(weight[n-1] > w)
return memo[w][n] = knapsack(w, n-1);
return memo[w][n] = max(knapsack(w, n-1), value[n-1] +
knapsack(w - weight[n-1], n-1));
}Problema da Mochila – Bottom Up
for(int i=0; i<=n; i++)
dp[i][0] = 0;
for(int j=0; j<=w; j++)
dp[0][j] = 0;
for(int i=1; i<=n; i++){
for(int j=1; j<=w; j++){
if(weight[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i-1]] + value[i-1]);
}
}Mochila: otimizando espaço
- Em nossa solução, estamos utilizando uma matriz 𝑑𝑝[𝑀𝐴𝑋_𝑊, 𝑀𝐴𝑋_𝑁].
- Dependendo do problema, isso pode ocasionar estouro de memória.
- Existem algumas formas de otimizar nossa solução para não precisarmos de uma matriz tão grande. Veja algumas delas nos seguintes links:
https://www.geeksforgeeks.org/space-optimized-dp-solution-0-1-knapsack-problem
https://codeforces.com/blog/entry/47247?#comment-316200
https://medium.com/@ThatOneKevin/knapsack-problems-part-1-8465fb2d53e9
Mochila ilimitada (com repetição)
- Uma variação comum do Problema da Mochila.
- Neste caso podemos considerar que temos uma quantidade ilimitada de cada item. Sendo assim, um mesmo item pode ser colocado mais de uma vez dentro da mochila.
Mochila ilimitada (com repetição)
- A ideia da nossa solução não irá se alterar muito. De certa forma, será até mais simples.
- Para uma certa capacidade 𝑖 da mochila, verificamos todos os itens 𝑗 que podem ser colocados nela (𝑤[𝑗] <= 𝑖) e qual resulta em maior valor (𝑣[𝑗] + 𝑑𝑝[𝑖 − 𝑤[𝑗]])
Mochila ilimitada (com repetição)
int knapsack(int n, int w){
memset(dp, 0, sizeof(dp));
for(int j=1; j<=w; j++){
for(int i=1; i<=n; i++){
if(weight[i-1] <= j)
dp[j] = max(dp[j], dp[j-weight[i-1]] + v[i-1]);
}
}
return dp[w];
}Diving for Gold (UVA - 990)
- Problema: Dado 𝑛 tesouros representados por pares (profundidade, quantidade de ouro)
- Para pegar um tesouro, leva-se 3 ∗ 𝑤 ∗ 𝑝𝑟𝑜𝑓𝑢𝑛𝑑𝑖𝑑𝑎𝑑𝑒 segundos (sendo 𝑤 uma constante dada pela entrada)
- Temos um cilindro de ar que nos permite ficar 𝑡 segundos submersos.
- Objetivo: determinar o máximo de tesouros que podemos pegar, e quais são estes tesouros.
Referências
Rene Pegoraro. Aulas de Técnicas de Programação.
Rene Pegoraro e Wilson M. Yonezawa. Aulas de Algoritmos Avançados.
Thiago Alexandre Domingues de Souza. Palestra sobre Programação Dinâmica.
Giulia Moura, João Pedro Comini e Pedro H. Paiola. Aulas de Programação Competitiva I.
Bruno Papa, Maurício Scarelli e Rodrigo Rosseti. Seminário sobre Programação Dinâmica.
LAAKSONEN, A. Competitive Programmer’s Handbook.
https://www.ime.usp.br/~pf/analise_de_algoritmos/aulas/dynamic-programming.html
http://www.decom.ufop.br/anderson/2_2012/BCC241/ProgramacaoDinamica.pdf
https://www.geeksforgeeks.org/tabulation-vs-memoizatation/
https://www.geeksforgeeks.org/solve-dynamic-programming-problem/
https://www.geeksforgeeks.org/longest-common-subsequence-dp-4/
https://neps.academy/lesson/164
http://www.facom.ufms.br/~marco/analise2007/aula12_4.pdf
https://github.com/icmcgema/gema/blob/master/09-Programacao_Dinamica.ipynb
https://www.ime.usp.br/~pf/analise_de_algoritmos/aulas/mochila-bool.html
https://www.geeksforgeeks.org/space-optimized-dp-solution-0-1-knapsack-problem
https://www.geeksforgeeks.org/unbounded-knapsack-repetition-items-allowed