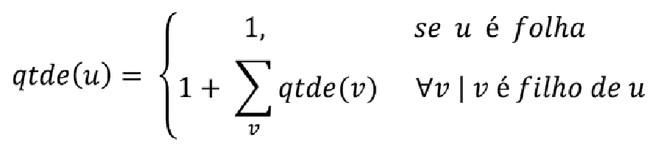01 - Árvores
Vértices ligados entre si
Autor(es): Pedro Henrique Paiola, Rene Pegoraro, Wilson M Yonezawa, Toki Yoshida, Nick Papi Barbosa Gomes, Pseudo-Pedro Henrique Morelli
Introdução
Fundamentos
- Um grafo é um estrutura de dados que consiste em um conjunto de nós (também denominados vértices) conectados entre si aos pares por arestas;
- As árvores são um subconjunto dos grafos que apresentam características específicas.
- Essas propriedades especiais permitem criar algoritmos especializados mais eficientes que os aplicados aos grafos gerais.
Definição
- Uma árvore é um grafo formado por N vértices indexados, ligados entre si por N – 1 arestas;
- Ambas as características acima garantem que a árvore seja:
- Acíclica: não possuem ciclos, assim, só acessamos cada nó na árvore uma única vez;
- Conexa: entre quaisquer dois nós pertencentes a árvore existe um caminho.
Terminologia
Conceitos
- Pai: nó antecessor de um determinado nó. Cada nó possui apenas um único pai.
- Filho: nó sucessor de um determinado nó. Um nó pai pode ter vários filhos.
- Raiz: "O pai de todos". Primeiro nó da árvore, aquele que dá origem aos demais, portanto, o único que não possui antecessor.
-
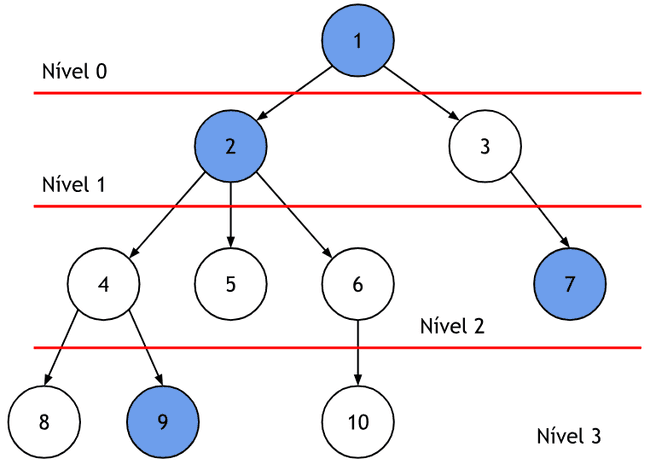
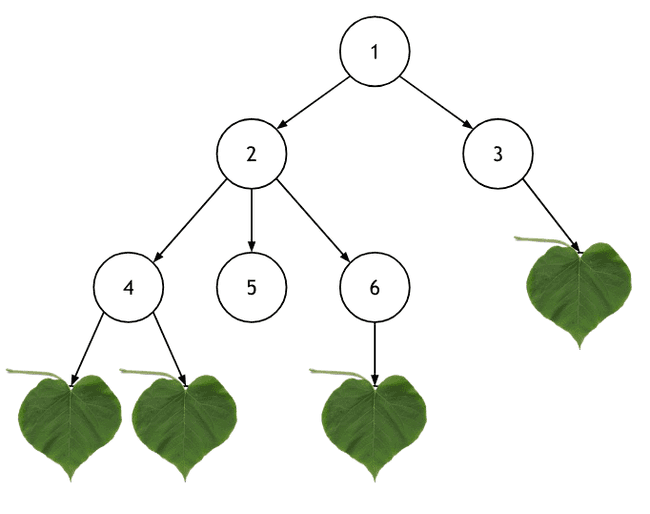
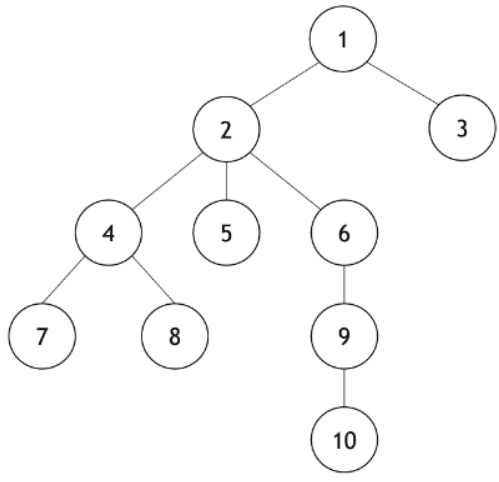
Nível de um nó: distância que um nó tem em relação a raiz, ou seja, a quantidade de arestas entre eles.
-
Exemplos:
Nível[1] = 0
Nível[2] = 1
Nível[7] = 2
Nível[9] = 3
- Altura da árvore: quantidade de níveis, a partir da raiz, até o nó mais distante.
- Na árvore ao lado, altura = 3.
- Folha: nó que não possui filhos.
-
Grau de um nó: número de ramificações, ou seja, de filhos de determinado nó.
-
Exemplos:
Grau[1] = 2
Grau[2] = 3
Grau[6] = 1
- Grau de uma árvore: número máximo de ramificações de um nó da árvore.
- Na árvore ao lado, grau = max{grau[nó] | ∀ nó da árvore}, portanto, grau da árvore = 3.
- Sub-árvore: qualquer árvore contida na árvore original.
Tipos de Árvores
Árvore Enraizada
- Uma árvore é enraizada quando há um nó especial, denominado de raiz;
- Com exceção da raiz, todo nó é ligado por uma aresta a um, e apenas um, nó;
- Há um caminho único da raiz a cada nó.
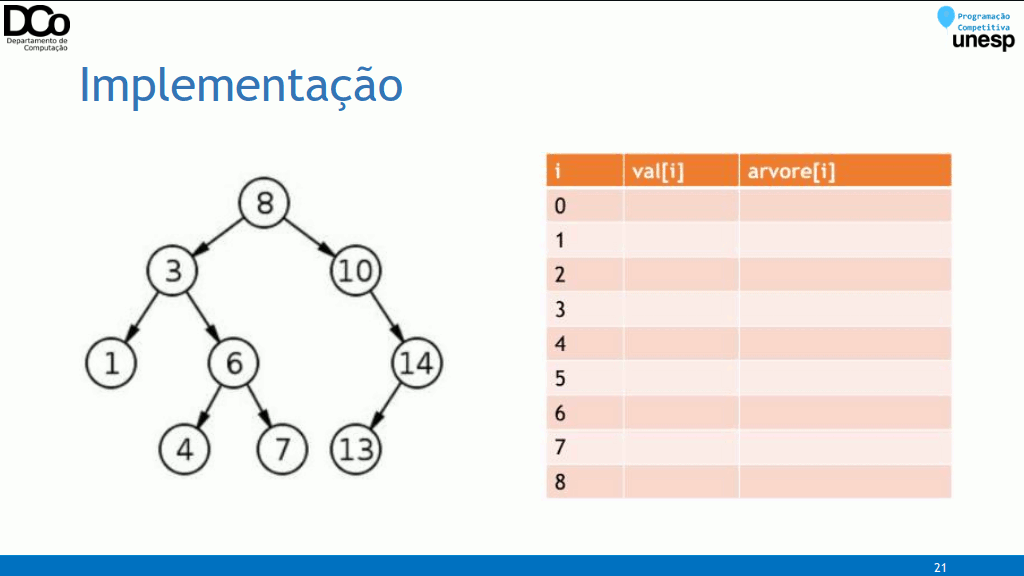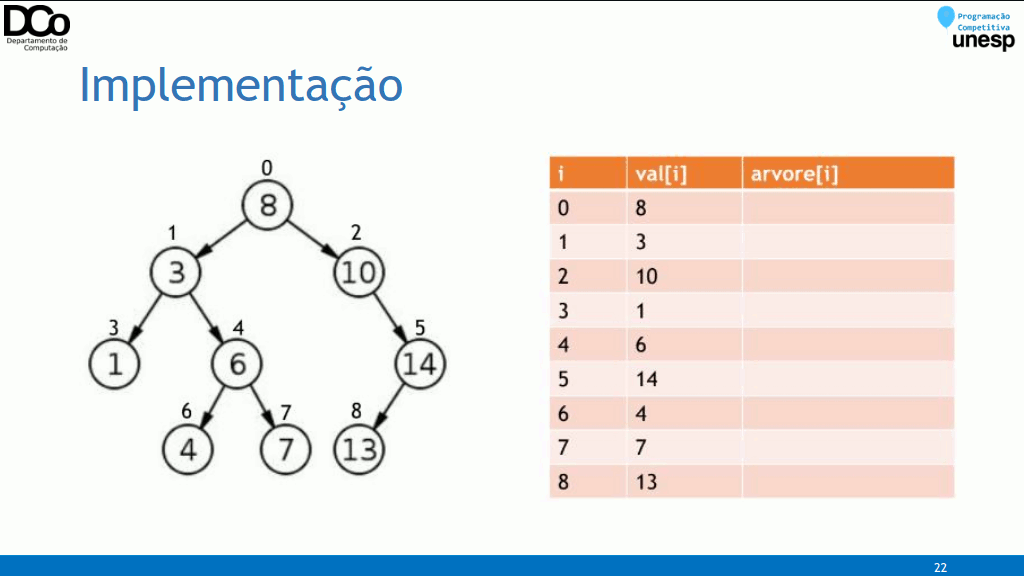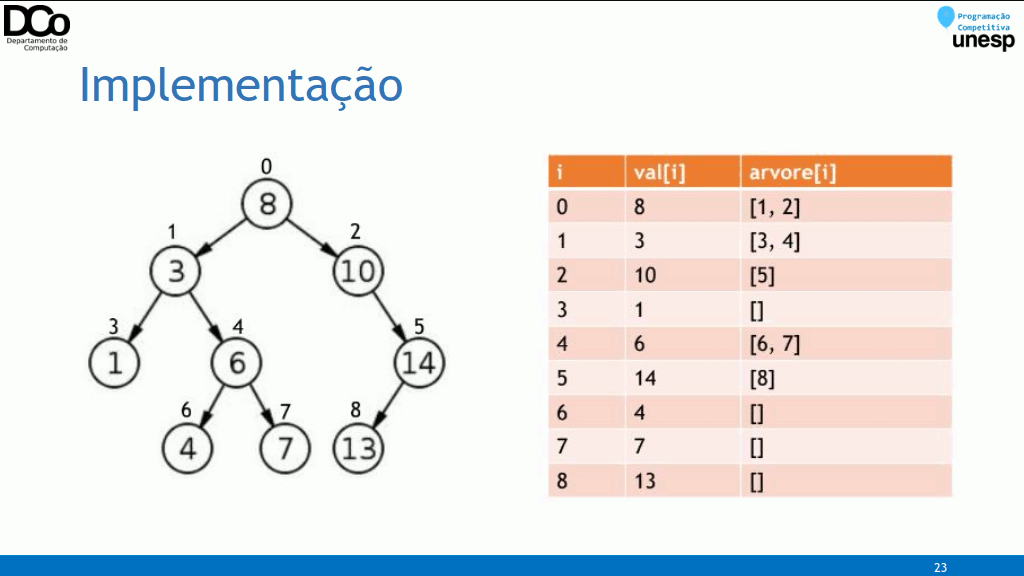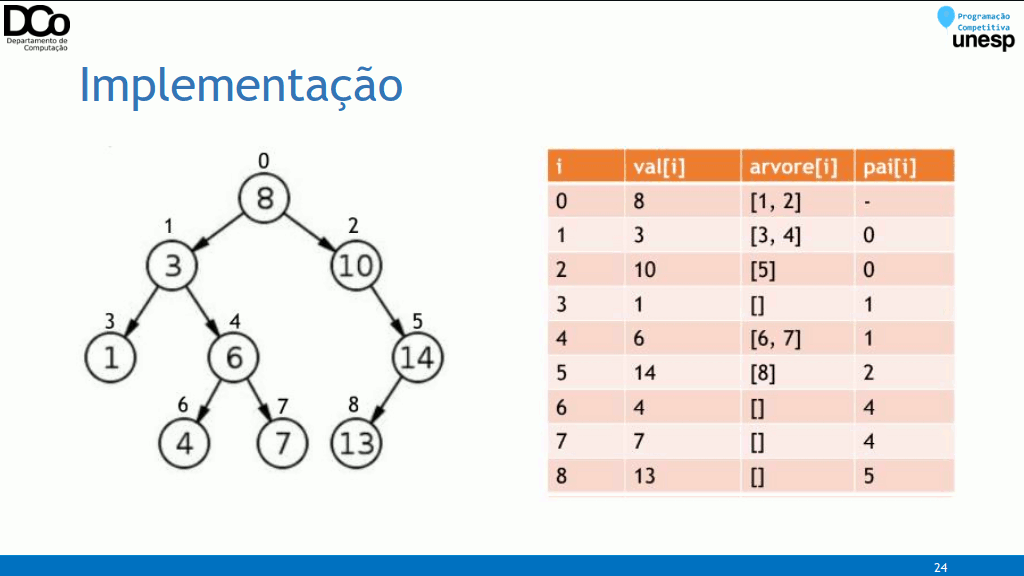
Implementação
- Existem várias formas de se implementar uma árvore, tanto com estruturas estáticas quanto dinâmicas;
- Qual a melhor representação depende muito do contexto em que a árvore será aplicada;
- Para as árvores enraizadas, a implementação é feita através de uma lista de adjacência, semelhante a implementação de grafos e aplicável na maioria dos casos.
vector<vector<int>> adj(qtd_vertices);
vector<int> parent(qtd_vertices);
void add_edge(int u, int v) {
// nó u pai é pai de v
adj[u].push_back(v);
parent[u] = v;
}- Confira na GIF abaixo:
Árvore Binária de Busca
- Uma Árvore Binária de Busca é uma árvore enraizada com as seguintes propriedades:
- Deve ter grau de árvore de, no máximo, 2;
- Para cada nó u, todos os nós da sub-árvore esquerda possuem valores menores que u, enquanto todos os nós da sub-árvore direita, valores maiores que u.
- Para sua implementação, utilizamos de ponteiros e alocação dinâmica de memória;
- Implementação:
struct Node {
int val;
Node *left, *right;
Node(const int &val) {
this->val = val;
left = right = null;
}
};
typedef Node *Tree;
void insert(Tree &tree, const int &val) {
if (tree != NULL) {
if (val < tree->val) {
insert(tree->left, val);
} else {
insert(tree->right, val);
}
} else {
tree = new Node(val);
}
}- Confira na GIF abaixo:

Algoritmos
Algoritmos de Busca
- Um algoritmo de busca (ou de varredura) é um algoritmo que visita todos os nós de um grafo ou árvore, andando pelas aresta de um vértice a outro;
- Uma varredura por si só não resolve um problema específico, mas serve de base para a resolução eficiente de vários problemas concretos.
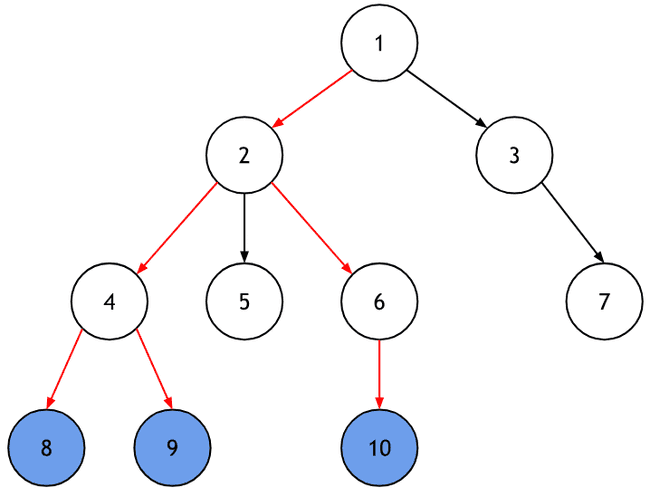
Busca em Profundidade (DFS)
- Na busca em profundidade (depth-first search), o algoritmo começa na raiz da árvore e explora tanto quanto possível cada um dos seus ramos antes de retroceder, representando uma ideia semelhante ao backtracking.
- Pode ser implementada tanto da maneira iterativa quanto da maneira recursiva;
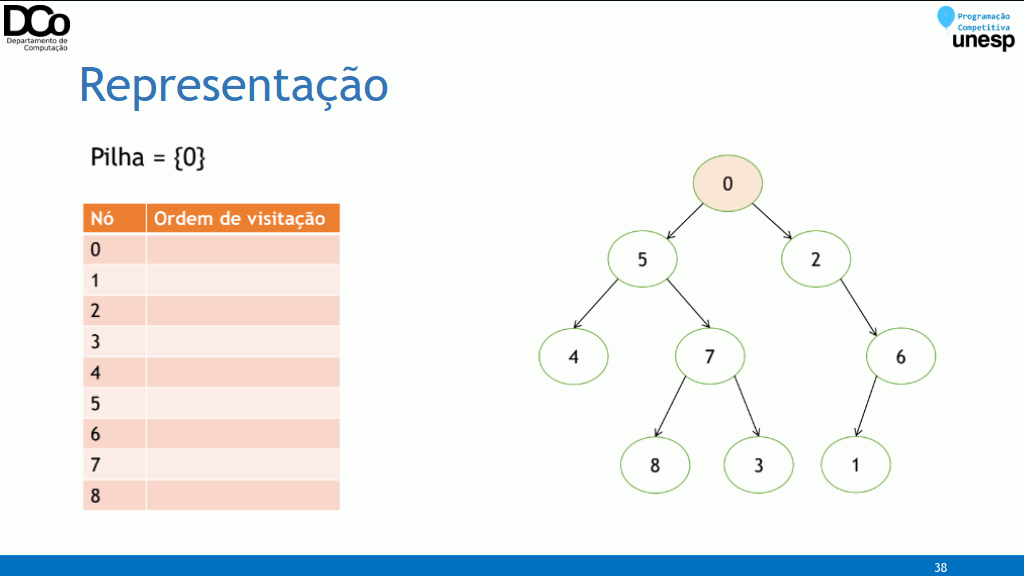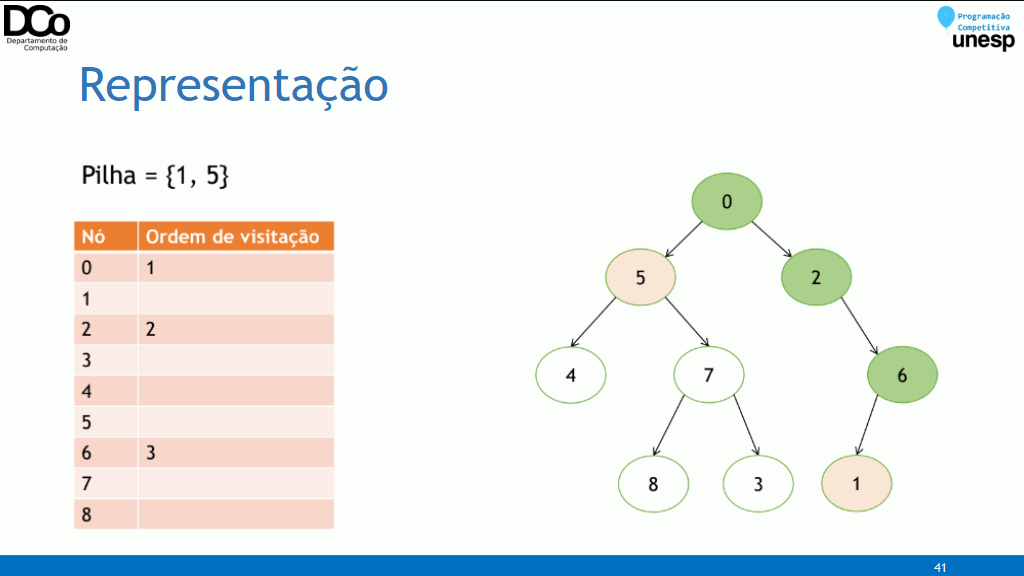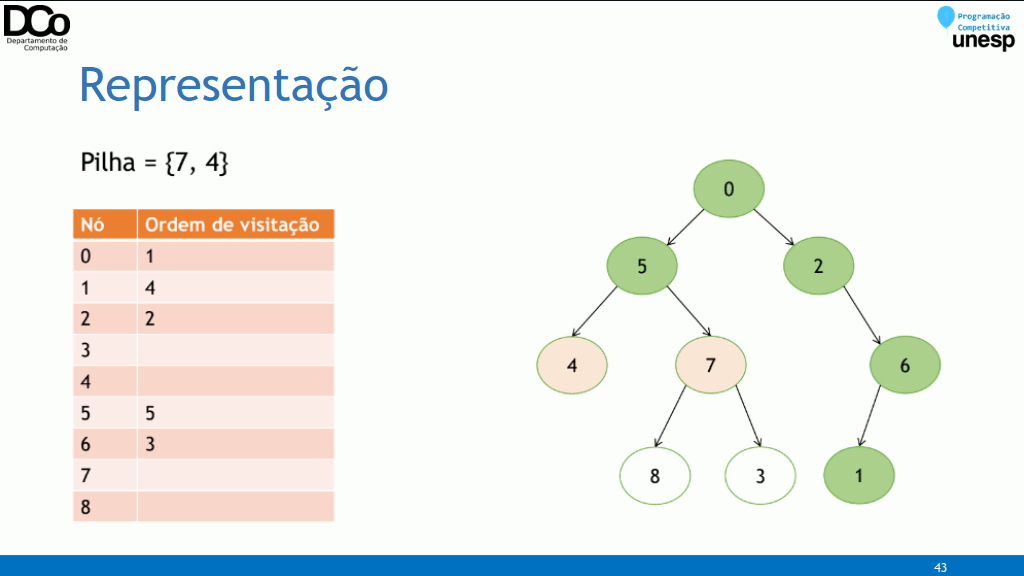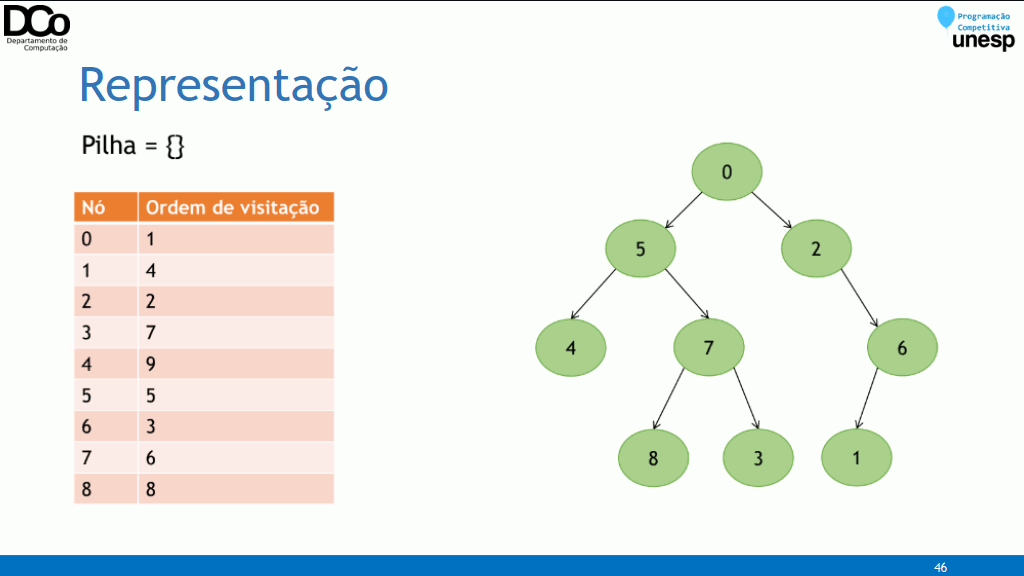
- Implementação Recursiva:
void dfs(int u, int parent) {
// processa o nó atual
for (int i = 0; i < adj[u].size(); i++) {
int v = adj[u][i];
if (v != parent)
dfs(u, v);
}
}
void dfs(int u, int parent) {
for (auto v: adj[u])
if (v != parent)
dfs(v, u);
}
void dfs(Tree tree) {
if (tree == NULL)
return;
// processa o nó atual
dfs(tree->left);
dfs(tree->right);
}- Implementação Iterativa:
void dfs(int root) {
stack<int> s;
s.push(root);
while(!s.empty()) {
int u = s.top();
s.pop();
// processa o nó atual
for(auto v : adj[u])
s.push(v);
}
}Busca em Largura (BFS)
-
Na busca em largura (breadth-first search), o algoritmo começa na raiz da árvore e explora nível a nível, isto é, inicialmente, a raiz é processada (nível 0), a seguir, todos os seus filhos (nível 1), então todos os filhos dos seus filhos (nível 2) e assim por diante;
-
A implementação da BFS é muito semelhante a versão iterativa da DFS, mas utilizando uma fila ao invés de uma pilha.
-
Confira na GIF abaixo:
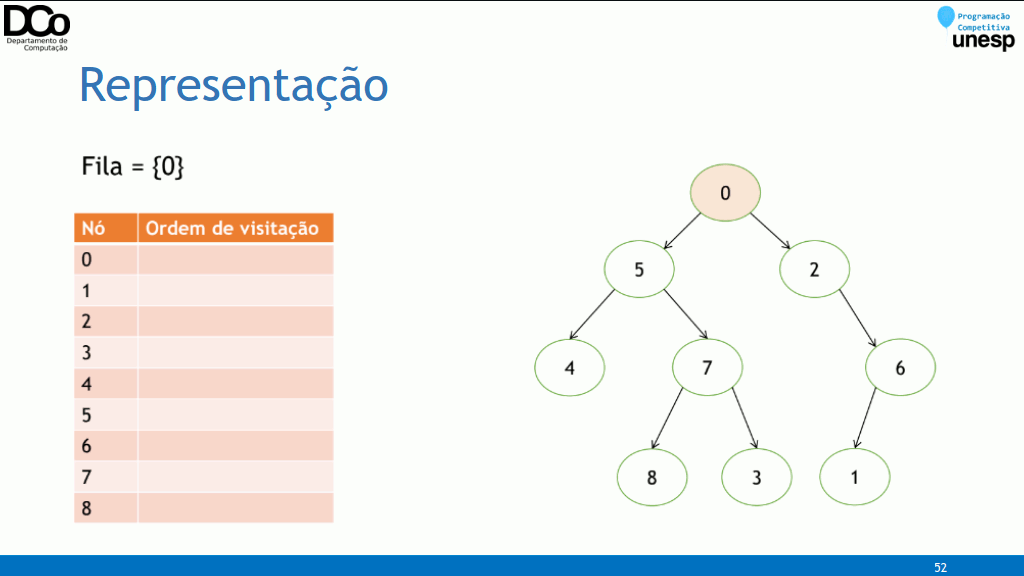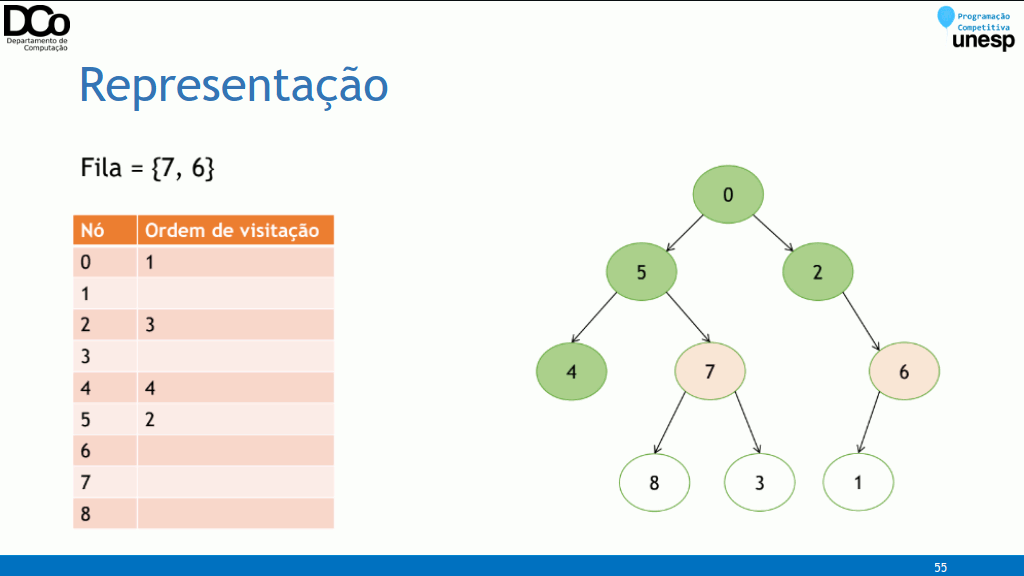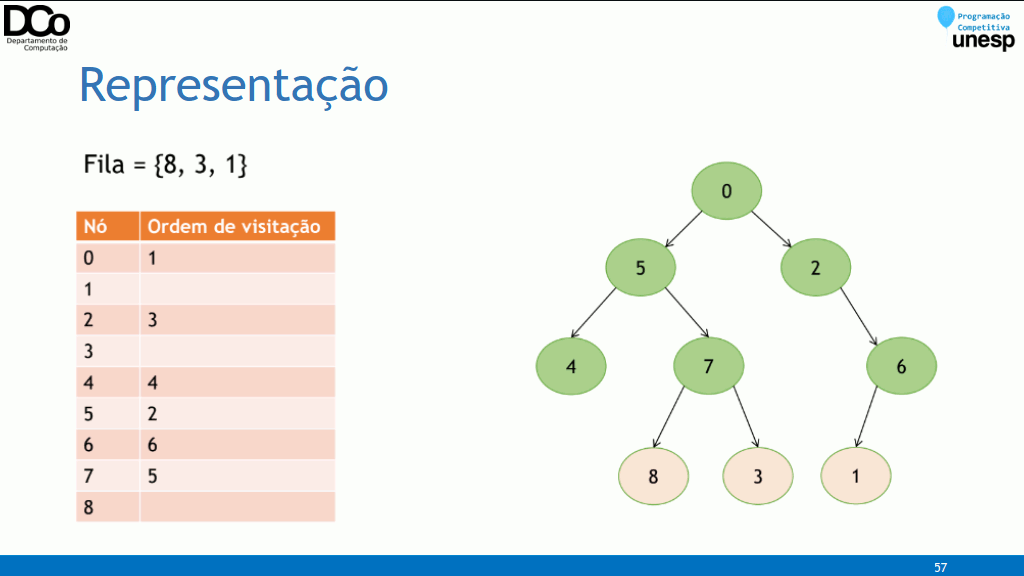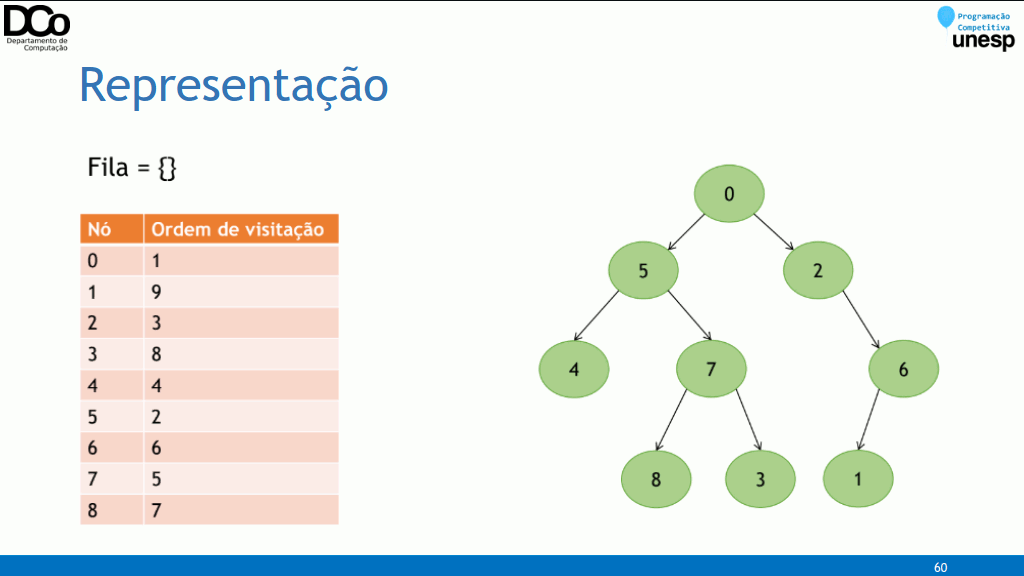
- Implementação:
void bfs(int root) {
queue<int> q;
q.push(root);
while(!q.empty()){
int u = q.front();
q.pop();
// processa o nó atual
for(auto v : adj[u])
q.push(v);
}
}Percurso em Árvore Binária
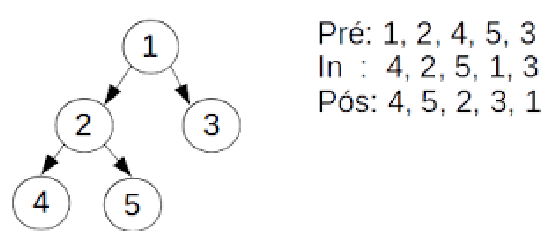
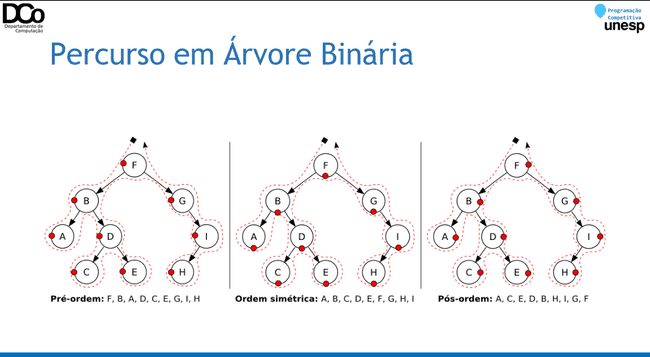
- Ao aplicar uma busca em profundidade em uma árvore binária, temos três opções de percurso, considerando a ordem de visitação da raiz (R), da sub-árvore da esquerda (E) e da sub-árvore da direita (D):
- Pré-ordem ou prefixo: R, E, D
- Em-ordem ou infixo: E, R, D
- Pós-ordem ou posfixo: E, D, R
Programação Dinâmica em Árvores
Árvores + Programação Dinâmica
- É comum a utilização de programação dinâmica para calcular certas informações durante uma varredura em uma árvore.
- Exemplo:
- Determinar a quantidade de nós em cada sub-árvore.
- Quantidade de nós na sub-árvore u:
int dfs(int u) {
counter[u] = 1;
for(auto v : adj[u])
counter[u] += dfs(v);
return counter[u];
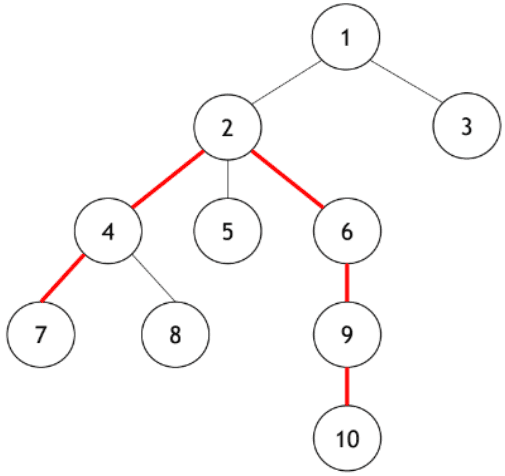
}PT07Z - Longest path in a tree
- O diâmetro de uma árvore é o maior comprimento de um caminho entre dois nós da árvore.
- Diâmetro da árvore ao lado: 5
Referências
LAAKSONEN, A. Competitive Programmer’s Handbook.
https://www.ime.usp.br/~pf/analise_de_algoritmos/aulas/dynamic-programming.html
http://www.decom.ufop.br/anderson/2_2012/BCC241/ProgramacaoDinamica.pdf
https://www.geeksforgeeks.org/tabulation-vs-memoizatation/
https://www.geeksforgeeks.org/solve-dynamic-programming-problem/