03 - Introdução à Teoria dos Grafos - Parte II

Caminho Mínimo

Autor(es): Pedro Henrique Paiola, Rene Pegoraro, Wilson M Yonezawa

Problema do Caminho Mínimo

Imagine o seguinte problema: dado um mapa de cidades, contendo o comprimento das estradas entre as cidades, qual o menor caminho entre quaisquer cidades A e B?
Esse problema pode ser modelado através de um grafo:
Cidades: vértices;
Estradas entre cidades: arestas ponderadas com peso que indicam a distância entre as cidades.
Generalizando, o nosso problema é encontrar o caminho de menor custo em um grafo de um vértice A até um vértice B.
Chamamos de custo de um caminho a soma dos pesos das arestas pertencentes a esse caminho.

Tipos de algoritmos utilizados para caminhos mínimos

Existem alguns algoritmos clássicos que resolvem tal problema:
Dijkstra
- Para pesos não negativos
- Complexidade: O(V + A log V)
Bellman-Ford
- Permite lidar com pesos negativos
- Complexidade: 𝑂(𝑉. 𝐴)
Floyd-Warshall
- Permite lidar com pesos negativos
- Encontra o menor caminho entre todo os pares de vértices (𝑢, 𝑣)
- Complexidade: 𝑂(𝑉3)

Algoritmo de Dijkstra

Este algoritmo parte de uma estimativa inicial para o custo mínimo e vai, iterativamente, ajustando esta estimativa.
A busca se inicia a partir de um vértice, a qual denominamos origem.
Ele considera que um vértice estará fechado quando já tiver sido obtido um caminho de custo mínimo da origem até ele. Caso contrário, ele é dito aberto.
Pseudocódigo: seja G(V, A) um grafo e 𝑠 um vértice de G(origem):

1. Atribua valor zero à estimativa de custo mínimo do vértice 𝑠 e ∞ às demais.
2. Enquanto houver vértice aberto:
	A. Seja 𝑘 um vértice ainda aberto cuja estimativa seja a menor entre 
    todos os vértices abertos: fechar o vértice 𝑘
	B. Para todo o vértice 𝑗 ainda aberto que seja adjacente à 𝑘 faça:
		i. Soma a estimativa do vértice 𝑘 com o custo da aresta 𝑘, 𝑗
		ii. Caso essa estimativa seja melhor que a anterior para 𝑗, 
        substitua e anote 𝑘 como precedente (“pai”) de 𝑗

Confira a GIF abaixo:

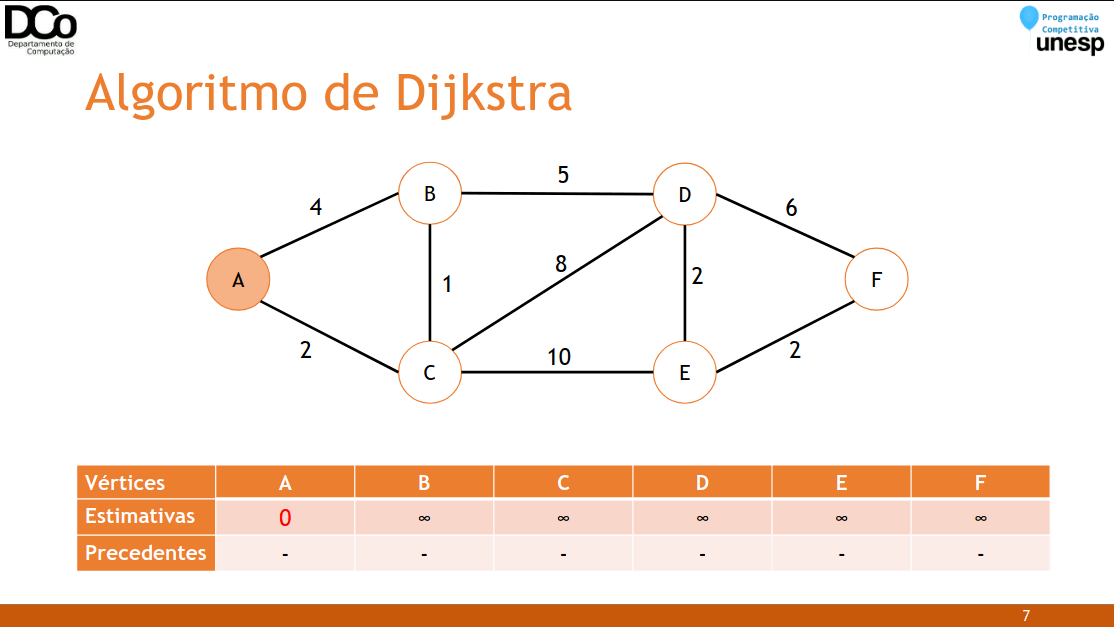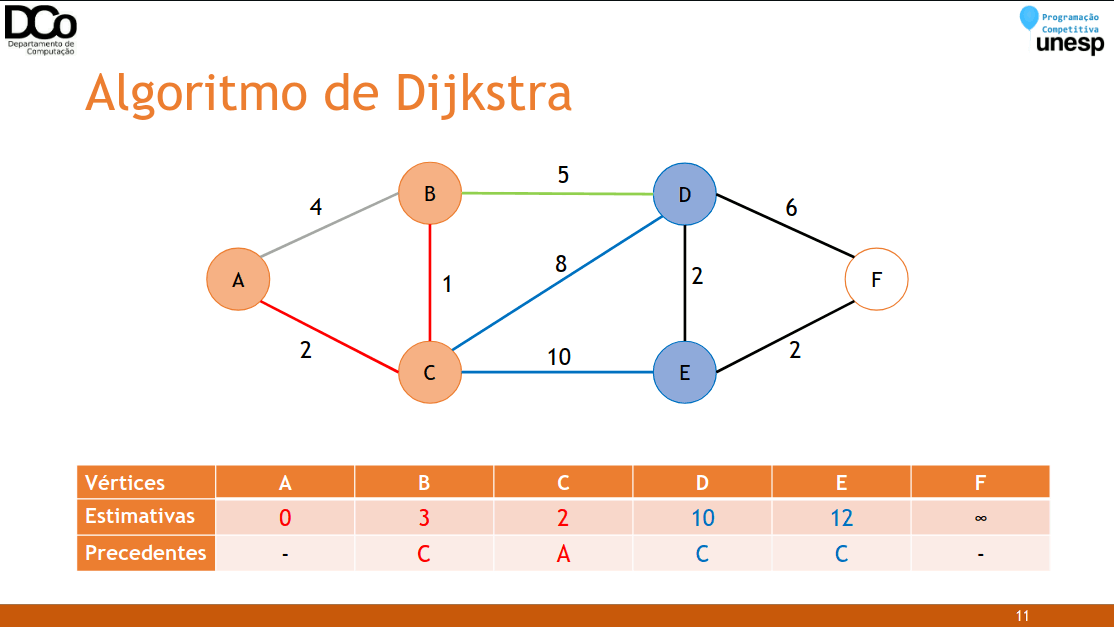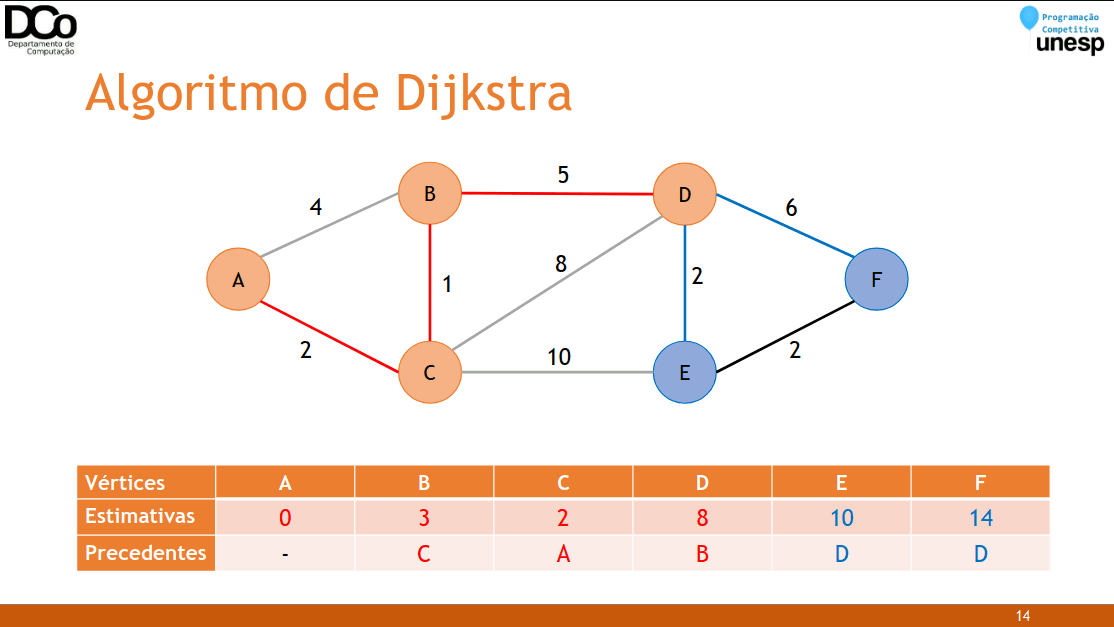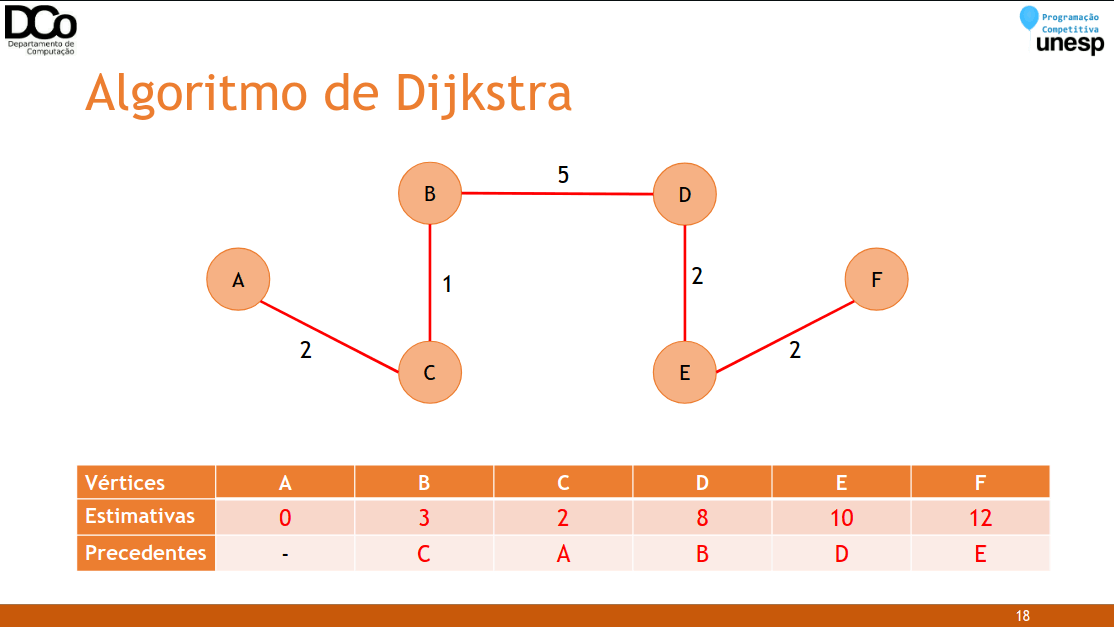
img1-img12

int d[MAX_V]; //d[i] armazena a distância até o vértice i, e as
//estimativas durante as iterações
int p[MAX_V]; //armazena o predecessor de cada vértice
void dijkstra(int inicial, int vertices){
    priority_queue< pair<int, int> > heap; //distância, vértice
    int s, t, peso;
    for(int i = 0; i < vertices; i++)
    d[i] = INT_MAX;
    memset(p, -1, sizeof(p));
    heap.push(make_pair(d[inicial] = 0, inicial));
    while(!heap.empty()){
        s = heap.top().second;
        heap.pop();
        for(int i = 0; i < grau[s]; i++){
            t = adj[s][i].v;
            peso = adj[s][i].w;
            if (d[s] + peso < d[t]){
            d[t] = d[s] + peso;
            p[t] = s;
            heap.push(make_pair(-d[t], t));
            }
        }
    }
}

Analisando a complexidade desse algoritmo de forma intuitiva, temos que (pensando no pior caso):
- Todos os vértices são fechados: |𝑉| operações
- Cada vez que um vértice é fechado, é porque ele foi extraído de uma heap: custo O(1) => O(|𝑉|)
- Para cada vértice, todas as suas arestas são acessadas. No total, acessaremos |𝐴| arestas ⇒ 𝑂(|𝑉| + |𝐴|)
- Cada vez que uma aresta é acessada, podemos inserir um elemento na heap: custo 𝑂(log |𝑉|) ⇒ 𝑂((|𝑉| + |𝐴|) ∗ log |𝑉|)
- Complexidade: 𝑂( (|𝑉| + |𝐴|) . log |𝑉|)

Caminho mínimo com arcos negativos

O algoritmo de Dijkstra se baseia em uma estratégia gulosa, e esta falha quando temos arestas com pesos negativos.
Quando fechamos o vértice aberto com menor distância até ele, estamos supondo que nenhum outro caminho até ele é menor.
Quando os pesos são não negativos, isso é verdade porque qualquer outro caminho irá utilizar arestas com peso maior ou igual a zero.
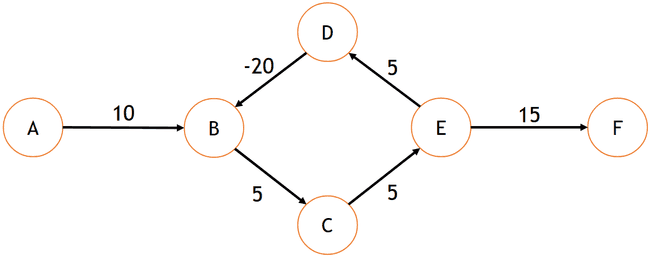
Porém, se existem arcos negativos, podemos ter caminhos que no momento apresentam um custo maior, mas posteriormente terão este custo reduzido pela adição de um arco negativo.
Confira a GIF abaixo:

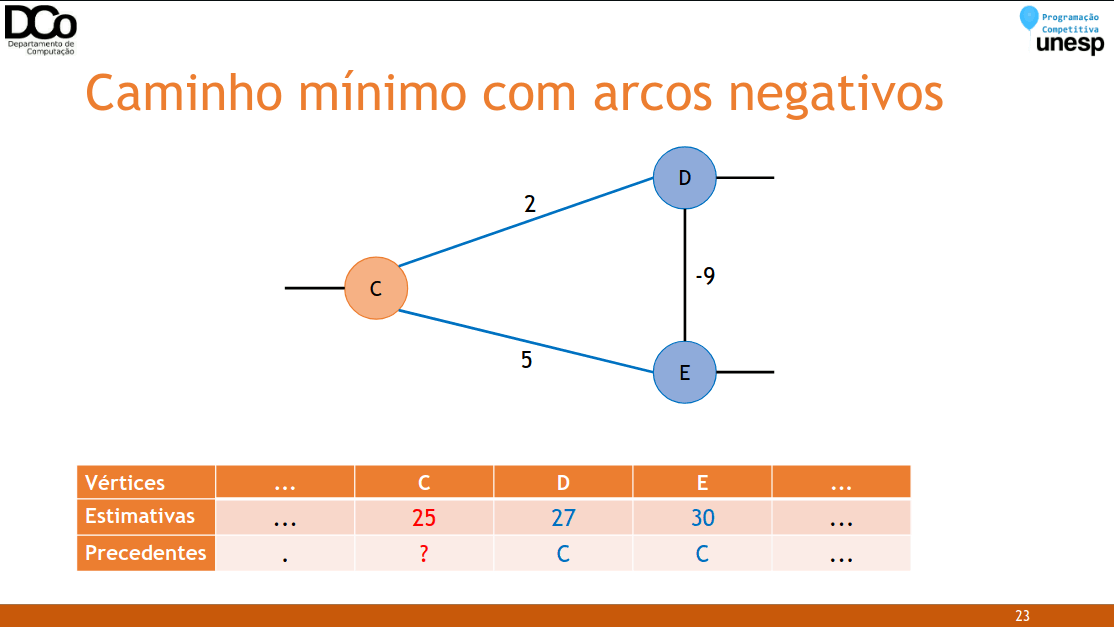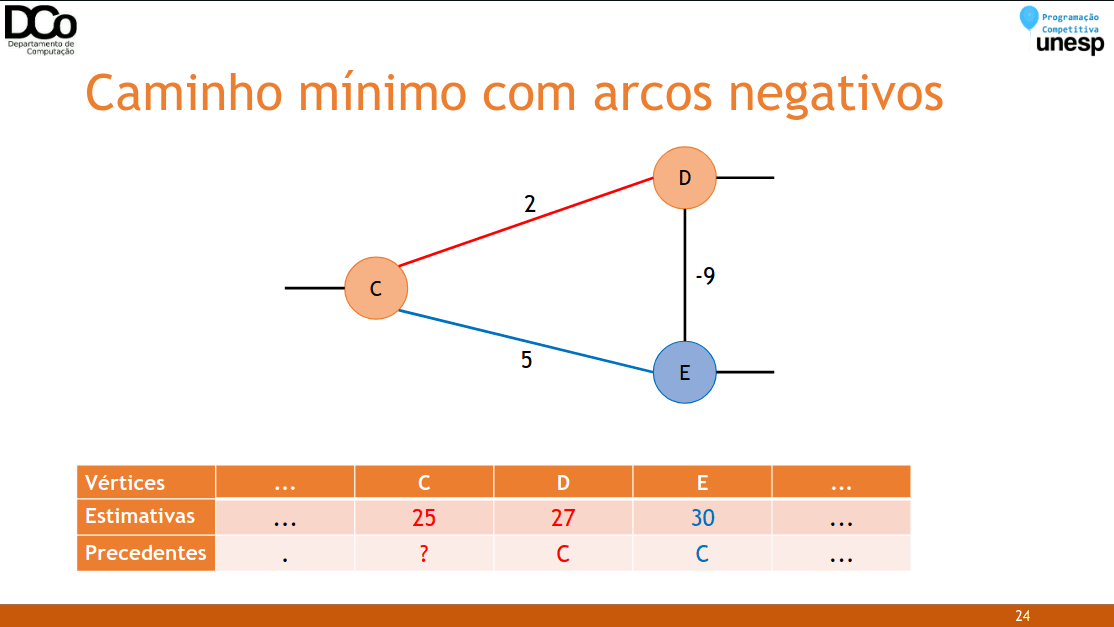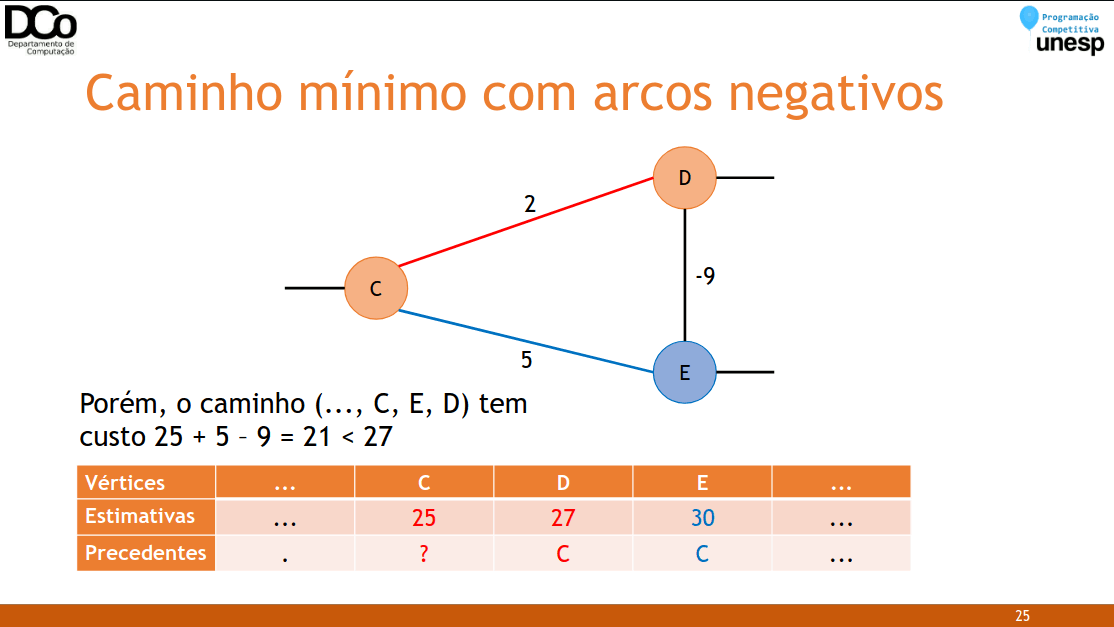
img13-img15

Quando pode aparecer arcos negativos em problemas de caminho mínimo?
Parece não fazer muito sentido falar em “distância” com arcos negativos, mas podemos ter diversos tipos de outros problemas em que esta situação se apresente.
Por exemplo: problemas envolvendo dinheiro, onde arcos positivos representam gastos e arcos negativos representam lucro. Nesse caso, um caminho mínimo maximiza o lucro.
Situação análoga: jogo em que os vértices representam estados, arcos positivos são transições que diminuem a pontuação do jogador, e arcos negativos são transições que aumentam a pontuação.
Caso insolúvel: presença de ciclos negativos
“Dar uma volta” em um ciclo de custo negativo sempre diminui o custo final.

Algoritmo de Bellman-Ford

Para encontrar um caminho mínimo em um grafo com a presença de arcos negativos, podemos utilizar o algoritmo de Bellman-Ford.
Se houver ciclos negativos, ele irá detectar.
O algoritmo de Bellman-Ford é dividido em três etapas:
Inicialização: padronização das distâncias
Relaxamento: cálculo efetivo dos caminhos mínimos
Verificação de ciclos negativos
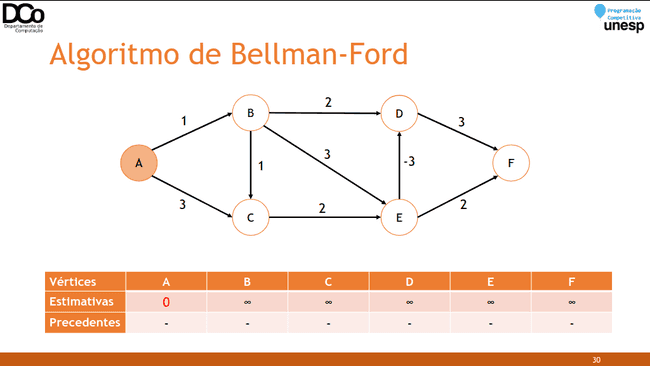
Inicialização: como no Dijkstra, a distância até a origem é inicializada com 0 e as outras como infinito.

Relaxamento: a técnica do relaxamento consiste em verificar se pode ser encontrado um caminho mais curto para 𝑣 passando por um certo vértice 𝑢:

se d[u] + peso(u, v) < d[v] então
d[v] = d[u] + peso(u,v)
p[v] = u

De forma semelhante ao Dijkstra, isso será feito 𝑉 − 1 vezes, porém considerando TODAS as arestas, e não apenas as incidentes no último vértice “fechado”.
Confira a GIF abaixo:

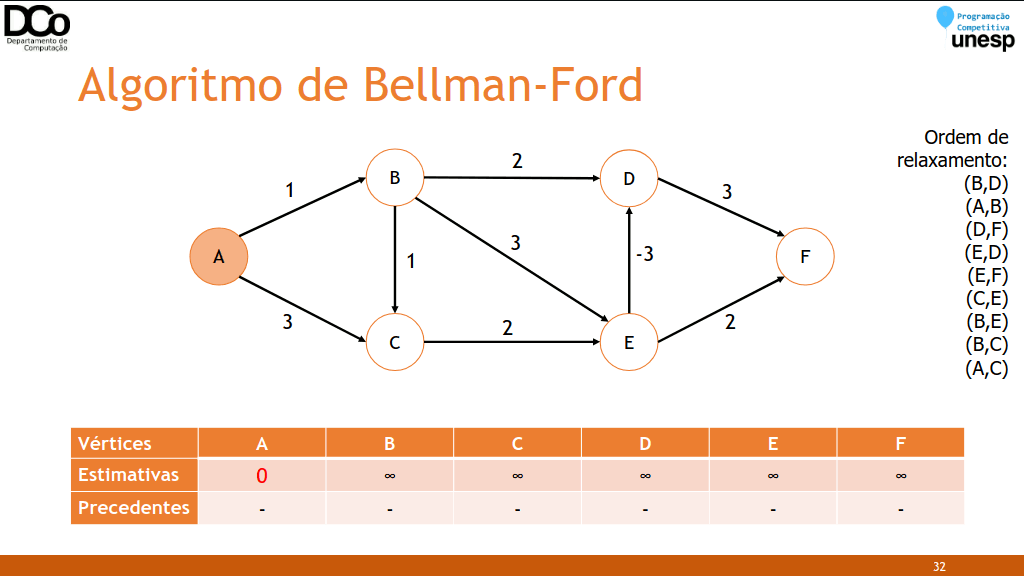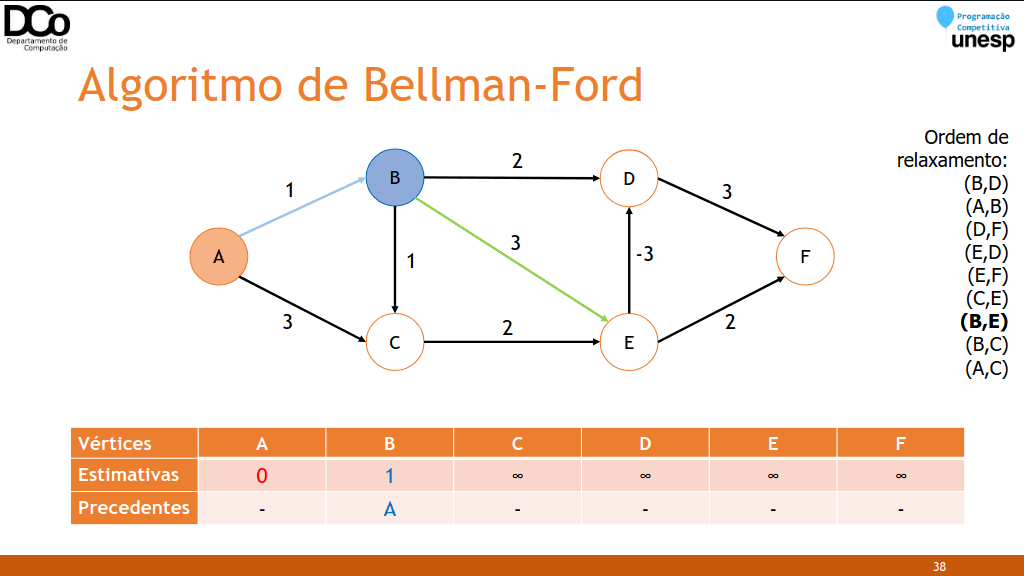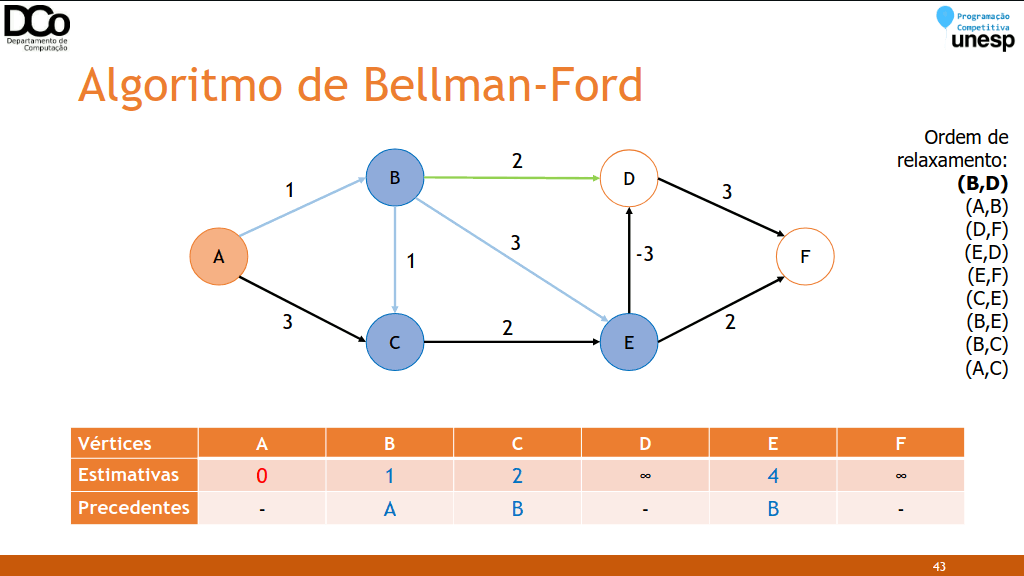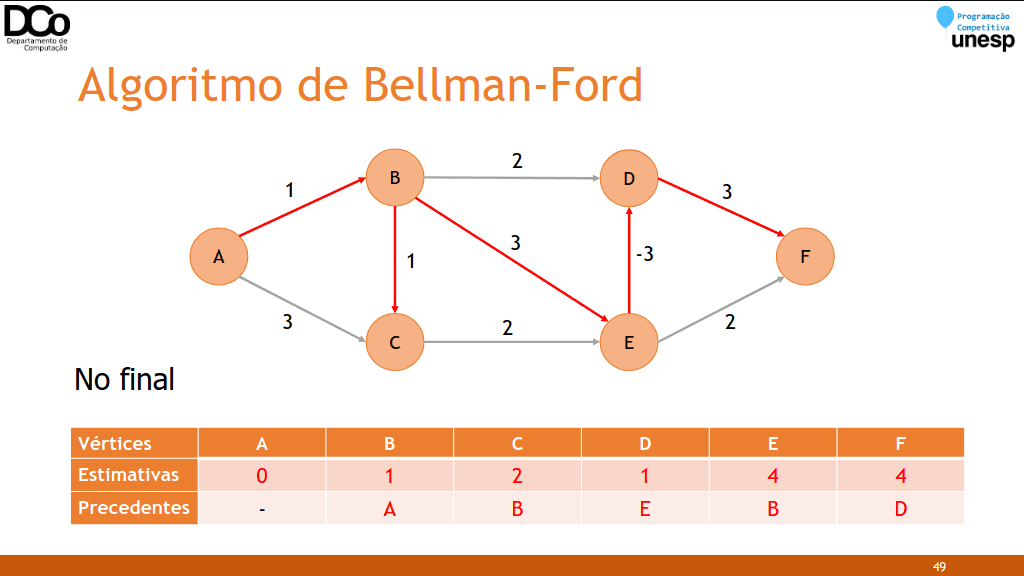
img18-img35

Checagem de ciclos negativos: o relaxamento é aplicado mais uma vez.
Se houver alguma situação em que se encontre caminho melhor, é por que temos a presença de um ciclo negativo.
Caso em que sempre pode-se encontrar um caminho menor, ao “andar” mais uma vez pelo ciclo.

BellmanFord(G, origem)
    d[v] = infinito, para todo v
    p[v] = -1, para todo v
    d[origem] = 0
    para i de 1 até |V(G)| - 1 faça
        para cada aresta (u,v) de G faça
            relax(u, v, w)
    para cada aresta (u,v) de G faça
        se d[v] > d[u] + peso(u,v)
            retorna FALSE
    retorna TRUE

bool bellmanFord(int inicial, int n){
    memset(p, -1, sizeof(p));
    for(int i=0; i<n; i++)
        d[i] = INF;
    d[inicial] = 0;
    for(int i = 0; i < n-1; i++){ //|V|-1 passos
        for(int j = 0; j < n; j++){ //para todas as
            if (d[j] == INF)
                continue;
            for(int k = 0; k < grau[j]; k++){ //arestas (j, k)
                if(d[j] + adj[j][k].w < d[adj[j][k].v])
                {
                    d[adj[j][k].v] = d[j] + adj[j][k].w;
                    p[adj[j][k].v] = j;
                }
            }
        }
    }
    //Verificando se há ciclo negativo
    for(int i=0; i<n; i++){
        if (d[i] == INF)
            continue;
        for(int j = 0; j < grau[i]; j++){
            if (d[adj[i][j].v] > d[i] + adj[i][j].w)
                return false;
        }
    }
    return true;
}

Caminho Euleriano

Um caminho euleriano é um caminho que percorre cada aresta de um grafo exatamente uma vez.
Um circuito ou ciclo euleriano é um caminho euleriano que começa e termina no mesmo vértice.
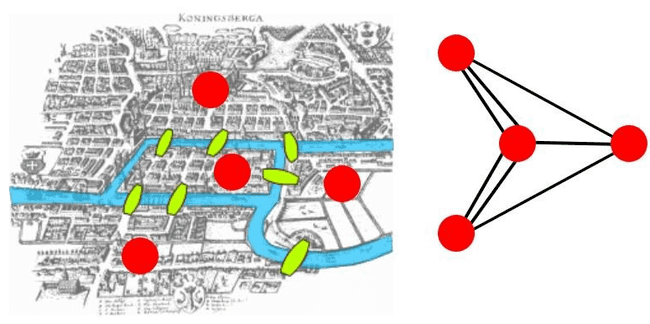
As sete pontes de Königsberg

Ao resolver o problema das sete pontes de Königsberg, Euler descobriu que existem critérios simples para determinar se um multigrafo tem um caminho ou ciclo euleriano:
Um multigrafo conexo com, pelo menos, dois vértices tem um ciclo euleriano se, e somente se, cada um de seus vértices tiver grau par.
Um multigrafo conexo tem um caminho euleriano (que não seja um ciclo) se, e somente se, tiver exatamente dois vértices de grau ímpar.
Aplicações em problemas práticos:
Problema do carteiro chinês: encontrar um caminho de menor custo que visite cada aresta do grafo ao menos uma vez.
Desenho de circuitos.
Redes de computadores de distribuição múltipla de dados.
Sequenciamento de DNA.
Problemas:
CodeForces 508D - Tanya and Password
URI 1671 - Código
URI 1053 - Desenho Contínuo

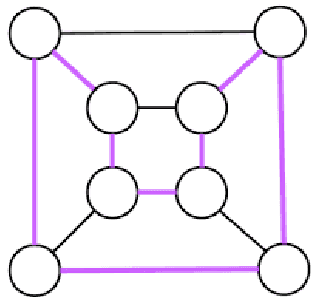
Caminho Hamiltoniano

Um caminho hamiltoniano de um grafo 𝐺 é um caminho que passa por todos os vértices de 𝐺 exatamente uma vez.
Um ciclo hamiltoniano é um caminho hamiltoniano que começa e termina no mesmo vértice.

A solução desse problema é mais complexa do que o problema do caminho euleriano. Já foram encontradas algumas condições suficientes para dizer se um grafo possui um caminho hamiltoniano, mas nenhuma condição necessária e suficiente.
O melhor algoritmo conhecido para encontrar um ciclo hamiltoniano (ou determinar se existe) tem complexidade exponencial.
Problema do Caixeiro Viajante: encontrar a menor rota que um caixeiro-viajante deveria tomar para visitar um conjunto de cidades.
Esse problema se reduz a encontrar um ciclo hamiltoniano em um grafo com o menor custo possível (custo = soma dos pesos das arestas do caminho).