02 - Exercícios

T-Primes, RSA Attack, DDF

Autor(es):

Resolução Exercícios Teoria dos Números

Exercício B, E e F

B - T-Primes

T-Primes são números positivos que tem exatamente 3 divisores distintos.
Dado n inteiros, determine quando os mesmo são ou não T-primes.
Entrada:

n (1 ≤ n ≤ 10^5 )
xi (1 ≤ xi ≤ 10^12 )

Como encontrar os T-Primes? Pela definição, conseguimos assumir que um número x é um T-prime, se seus divisores forem apenas: 1, (algum_numero_primo), x Por exemplo, um número primo, não é um T-prime, pois ele é divisível apenas por ele mesmo e 1.
Mas qual número primo se encaixa nessa configuração?

1 < (algum_numero_primo) < x

O único número que se encaixa nessa configuração seria um número primo multiplicado por ele mesmo que gerasse x, exemplo:

Para x = 9,
1 < 3 < 9

Solução: Dado um número n:

if (n == 1) cout << “NO”;
else if (quadrado_perfeito(n) && ehPrimo[sqrt(n)])
    cout << “YES”;
else
    cout << “NO”;

Para x = 16, 16 é um quadrado perfeito, mas como sqrt(16) = 4 e 4 não é um número primo, ficamos no final com mais de 3 divisores: 1,2,4,8,16

vector<bool> ehPrimo;
ll MAXN = 1000000;
void crivo()
{
    ehPrimo = vector<bool>(MAXN + 1, true);
    ehPrimo[0] = ehPrimo[1] = false;
    for (ll i = 2; i * i <= MAXN; i++)
    {
        if (!ehPrimo[i])continue;
        for (ll m = i * i; m <= MAXN; m += i)
        ehPrimo[m] = false;
    }
}

E - RSA Attack

O enunciado nos apresenta o seguinte problema
- Achar um inteiro m que satisfaça a equação: m^e (mod n) = c (mod n)
- Onde:
- n é o produto de dois números primos ímpares, p e q
- gcd(e, (p - 1)(q - 1)) = 1
- e < (p - 1)(q - 1)
- e, n, c <= 32000
1ª ETAPA: manipular a equação
- Precisamos encontrar o valor de m, mas, no estado atual de nossa equação, temos apenas o valor de me, logo, queremos eliminar essa potência.

me (mod n) = c (mod n)

elevar ambos os lados da equação por x

(me)x (mod n) = (c)x (mod n)

mex (mod n) = cx (mod n)

Podemos, então, supor que ex = 1, pois, assim, mex = m1.
Assim, temos: m (mod n) = cx (mod n)
Agora, sabemos que o valor de m é o resultado da potência cx.
Contudo, não sabemos o valor de x, portanto precisamos encontrá-lo.
2ª ETAPA: encontrar o valor de x
- Para tal, vamos utilizar as seguintes afirmações do exercício:
  1. ex = 1
  2. gcd(e, (p - 1)(q - 1)) = 1
  3. e < (p - 1)(q - 1)
Podemos perceber, pelas afirmações 1 e 2, que:

ex = gcd(e, (p - 1)(q - 1)) = 1

Uma equação diofantina tem o formato:

ax + by = c

E sabemos que podemos resolver através do algoritmo estendido de

Euclides equações diofantinas com a seguinte configuração;

ax + by = gcd(a, b) = c

Comparando nossa equação atual com a equação diofantina geral:

ex = gcd(e, (p - 1)(q - 1)) = 1 (I)

ax + by = gcd(a, b) = c (II)

Percebemos que:

a = e

b = (p - 1)(q - 1)

c = 1

Portanto, podemos escrever nossa equação como:

ex + (p - 1)(q - 1)y = gcd(e, (p - 1)(q - 1)) = 1

E descobrimos os valores de x e de y aplicando o algoritmo estendido de Euclides.
O exercício nos garante que encontraremos uma solução para o problema, então não precisamos nos preocupar com isso.
3ª Etapa: definir os valores para p e q
- Os valores de p e q não estão definidos para aplicarmos na equação que obtemos, porém sabemos que n = p * q.
- Assim, testamos valores de p e q da seguinte maneira:
1. Dado um número p, verificamos se p é primo.
2. Se p é primo, verificamos se a divisão n / p é inteira por meio da expressão n % p == 0.
3. Se a divisão for inteira, verificamos se o valor q = n / p também é primo.
4. Se todos os itens anteriores forem verdadeiros, encontramos p e q.
Cuidados:
x pode ser um valor negativo na resolução da equação diofantina, pois se uma solução é possível, elas admitem infinitas soluções.
Porém, temos que:

e < (p - 1)(q - 1) (I)

ex = 1 -> e = 1 / x (II)

Para garantir I, podemos reescrever II como:

e (mod (p - 1)(q - 1)) * x = 1

Aplicando propriedades da álgebra modular, obtemos:

ex (mod (p - 1)(q - 1)) = 1 (mod (p - 1)(q - 1))

Assim, e levando em consideração que x é a multiplicativa inversa de e, podemos concluir que:

e, x < (p - 1)(q - 1) = mod

Se x < 0, x = (x % mod + mod) % mod

Senão, x = x % mod

vector<bool> is_prime;
vector<int> primes;
void crivo(const int &n) {
    is_prime = vector<bool>(n + 1, true);
    is_prime[0] = is_prime[1] = false;
    for (int i = 2; i * i <= n; i++) {
        if (is_prime[i]) {
            for (int j = i * i; j <= n; j += i) {
                is_prime[j] = false;
            }
        }
    }
    for (int i = 2; i <= n; i++) {
        if (is_prime[i])
            primes.push_back(i);
    }
}

crivo(32000);
while (k--) {
    int e, n, c, p, q;
    cin >> e >> n >> c;
    for (int i = 0; i < m; i++) {
        p = primes[i];
        if (n % p == 0 && is_prime[n / p]) {
            q = n / p;
            break;
        }
    }
    int x, y, mod = (p - 1) * (q - 1);
    extended_gcd(e, mod, x, y);
    x = (x % mod + mod) % mod;
    cout << pow_mod(c, x, n) << "\n";
}

ll pow_mod(ll b, ll x, ll mod) {
    ll m = 1LL;
    while (x) {
        if (x & 1) {
            m = (m * b) % mod;
        }
        b = (b * b) % mod;
        x >>= 1;
    }
    return m;
}

F - DDF

É dado o início e o fim de um intervalo
O objetivo é saber qual o número com a maior sequência DDF nesse intervalo.
DDF -> Decimal Digit Factor Sequence
Confira na GIF abaixo:

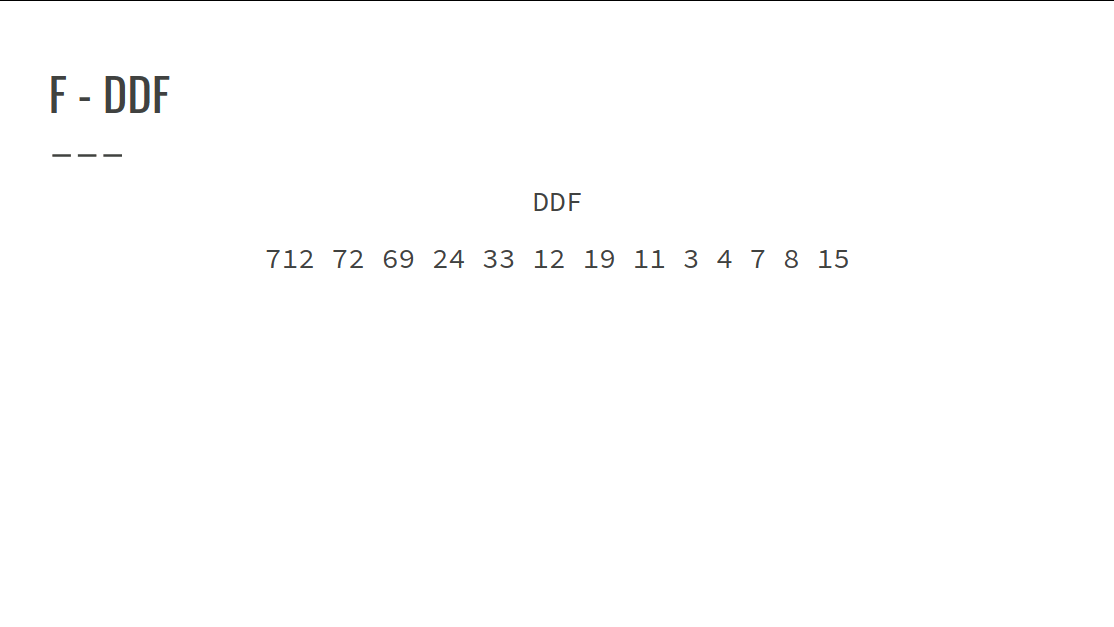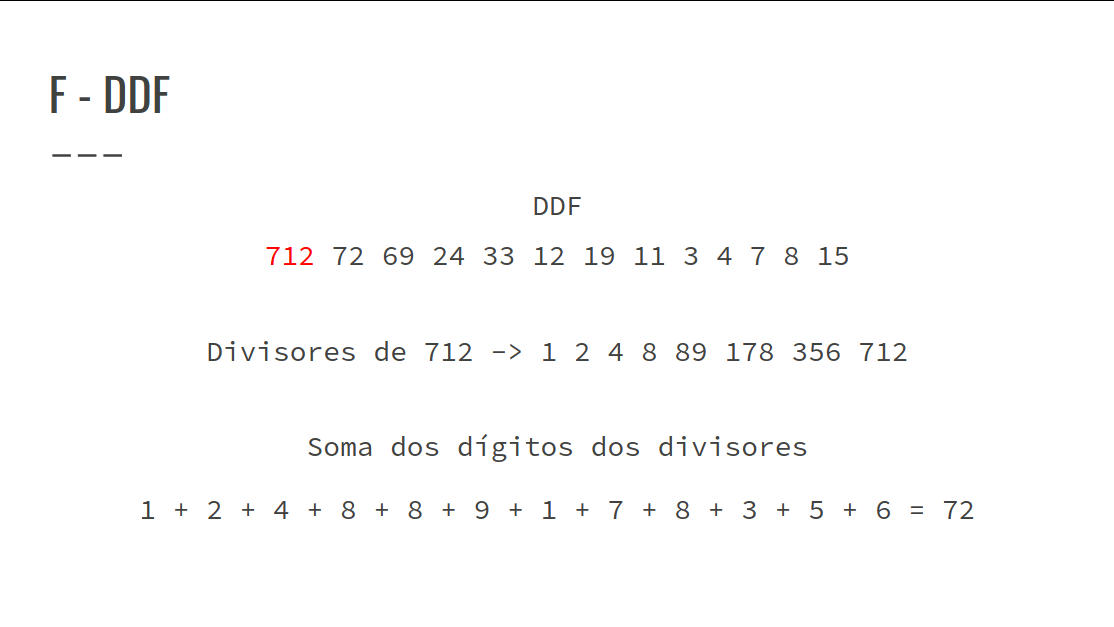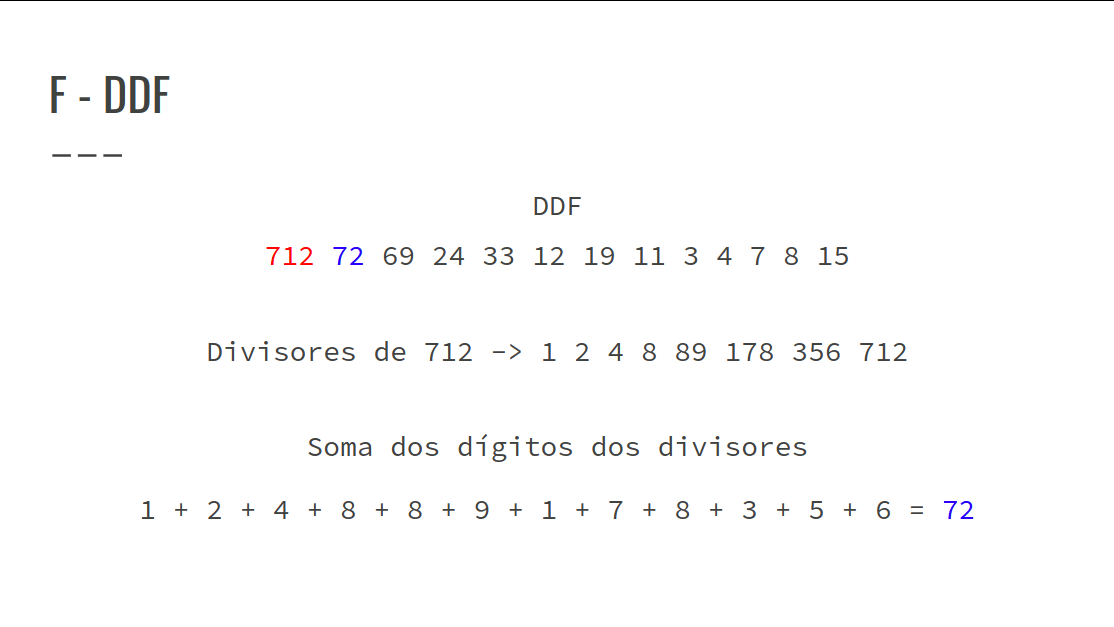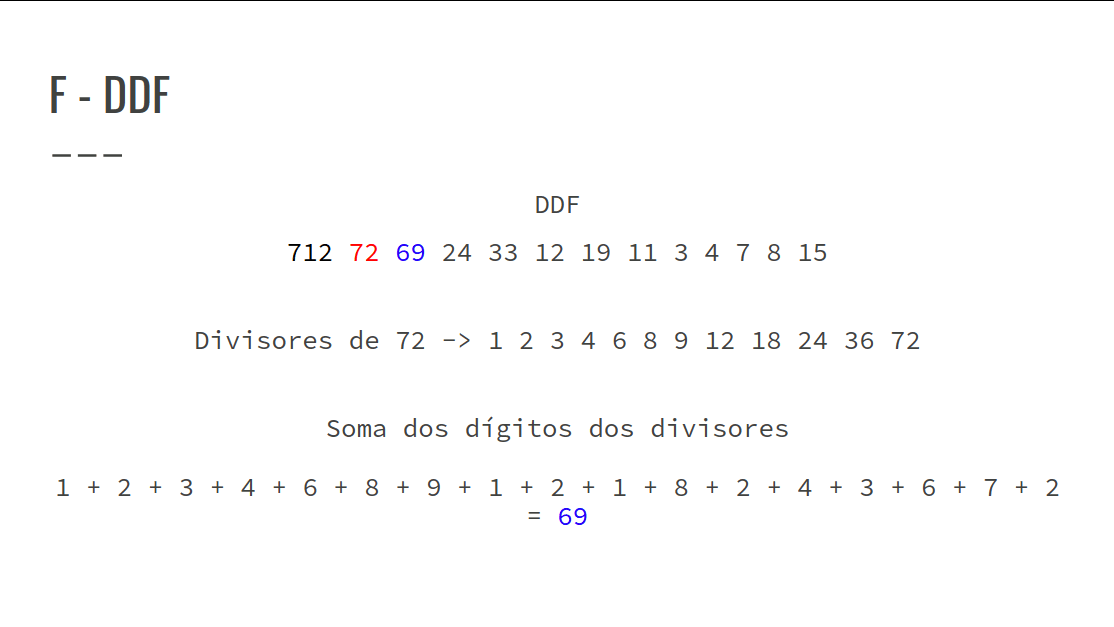
img1-img4

Objetivo: Encontrar a maior DDF no intervalo dado.
Como o intervalo vai de 1 a 3000 no máximo e o tamanho de uma DDF é no máximo 1000, pode-se calcular todas as DDFs, de maneira offline, e pegar a maior.

ll soma_digitos(ll num){
    ll sum = 0;
    while(num){
        sum += num%10;
        num/=10;
    }
        return sum;
}
ll fatorar(ll n){
    vector<ll> fator;
    ll soma = 0;
    for (ll i = 1; i * i <= n; i++){
        if(n%i == 0){
            if(n != i*i)soma += soma_digitos(n/i);
            soma += soma_digitos(i);
        }
    }
    return soma;
}
vector<ll> ddf [3001];
for(int i = 1; i <= 3000; i++){
    ll ant = i, res = i;
    ddf[i].push_back(i);
    while(1){
        res = fatorar(res);
        if(ant == res)break;
        ddf[i].push_back(res);
        ant = res;
    }
}