01 - Introdução à Teoria dos Números

Propriedades dos números

Autor(es): Pedro Henrique Paiola, Rene Pegoraro, Wilson M Yonezawa, Arissa Yoshida, Nicolas Barbosa Gomes, Luis Henrique Morelli

BigInteger

Certos problemas da Maratona de Programação recebem como entrada números inteiros que extrapolam o limite de variáveis do tipo long long int
Tamanho de uma variável long long int: 8 bytes
Intervalo de números que podem ser armazenados em uma variável desse tipo:
-9.223.372.036.854.775.808 à 9.223.372.036.854.775.807
0 à 18.446.744.073.709.551.615 (unsigned long long int)
Certos problemas da Maratona de Programação recebem como entrada números inteiros que extrapolam o limite de variáveis do tipo long long int
Exemplo: 2667 - Jogo de Boca
- Entrada: 𝑁 (3 ≤ 𝑁 ≤ 10¹⁰⁰)
1ª Situação: dependendo das operações necessárias de se fazer com o número, podemos ler o número como sendo uma string e trabalhar com essa string.
Exemplos:
- Operações simples com dígitos
- Uso de Aritmética Modular
2ª Situação: se precisarmos fazer operações com esse número como soma, subtração, multiplicação e divisão, o problema se torna mais complexo.
Nesses casos, não recomendamos usar a linguagem cpp. É possível trabalhar com BigInteger em cpp (a biblioteca do Thiago traz códigos para isso), porém a quantidade de código necessária é relativamente grande.
Sugestões: Java ou Python
Em Java podemos usar a classe BigInteger da biblioteca java.math

String Num;
BigInteger NumGrande;
Scanner S = new Scanner(System.in);
Num = S.nextLine();
NumGrande = new BigInteger(Num);
NumGrande = NumGrande.mod(new BigInteger("3"));
System.out.println(NumGrande);

Em Python, não precisamos nos preocupar muito com o tamanho de um inteiro, a memória é alocada conforme o necessário para comportar o tamanho do número.
Entrada e Saída em Python
Python em Programação Competitiva
Muita coisa sobre Python
Em Python, não precisamos nos preocupar muito com o tamanho de um inteiro, a memória é alocada conforme o necessário para comportar o tamanho do número.

U = int(input())
print(U % 3)

Teoria dos Números

A Teoria dos Números é o ramo da matemática que se preocupa com as propriedades dos números inteiros.
Existe uma coleção de algoritmos interessantes derivados de estudos da Teoria dos Números que solucionam problemas de forma inteligente e eficiente.
Aqui faremos uma breve introdução à alguns tópicos relativos à Teoria dos Números.

Números primos

Diversos problemas envolvem o uso de números primos.
Dessa forma, precisamos, inicialmente, de uma forma de testar se um número é primo ou não.
Recordando: números primos são números naturais que têm apenas dois divisores: 1 e ele mesmo.
Algoritmo ingênuo 𝑂(𝑛)

bool ehPrimo(int n)
{
    for(int i = 2; i < n; i++)
    if (n % i == 0)
        return false;
    return true;
}

Porém, na verdade só precisamos testar até 𝒏
Demonstração:
- Suponha que não, nesse caso existe 𝒏 tal que o menor fator primo 𝒑 de 𝒏 é maior que sqrt(𝒏).
- Se 𝒑 divide 𝒏, então 𝒏/𝒑 também divide 𝒏, e 𝒏/𝒑 deve ser maior que sqrt(n).
- Mas se 𝒑 > sqrt(n) e 𝒏/𝒑 > sqrt(n) , então 𝒑 . 𝒏/𝒑 > 𝒏, o que é um absurdo!
Algoritmo 𝑂( sqrt(𝑛))

bool ehPrimo(int n)
{
    for(int i = 2; i*i <= n; i++)
        if (n % i == 0)
            return false;
    return true;
}

Crivo de Eratóstenes

O Crivo de Eratóstenes é um método de encontrar os números primos até um certo valor limite.
Útil em casos que faremos vários testes de primalidade e na fatoração de números.
Ideia geral: dado que um número 𝒑 é primo, marcamos os múltiplos de 𝒑 como não sendo números primos.
Algoritmo:

Cria-se uma lista de 2 a MAX, marcando todos como primos
Para cada número i de 2 até sqrt(MAX)
Se i está marcado como primo
Marcar todos os números múltiplos de i a partir de i . i 
como compostos (não primos)

Por que podemos marcar só a partir de 𝑖. 𝑖?

Antes de 𝒊. 𝒊 temos: 𝑖. 2, 𝑖. 3, 𝑖. 4, … 𝑖. (𝑖 − 1). Ou ainda, 𝒊. 𝒋 | 𝟐 ≤ 𝒋 < 𝒊
Seja 𝒙 = 𝒊. 𝒋, 𝒙 é múltiplo de 𝒊 e também é múltiplo de 𝒋
Todo 𝒋 ou é primo, ou é múltiplo de um número primo menor que 𝒊, ou seja, um primo já “descoberto” pelo algoritmo
Se 𝒋 é primo
- Todos os seus múltiplos foram marcados como não primo, inclusive 𝒊. 𝒋
Se 𝒋 é múltiplo de um primo 𝒑 < 𝒊
- Então ele já foi marcado como composto, por ser múltiplo de 𝒑, assim como todos os seus múltiplos
Logo, todos os números 𝒊. 𝒋 | 𝟐 ≤ 𝒋 < 𝒊 já foram marcados

bool ehPrimo[MAX];
vector<int> primos;
void crivo(int n){
    memset(ehPrimo, true, sizeof(ehPrimo));
    for(int p = 2; p * p <= n; p++){
        if (ehPrimo[p]){
            primos.push_back(p); //Lista incompleta, primos até sqrt(n)
            for(int i = p*p; i <= n; i += p)
            ehPrimo[i] = false;
        }
    }
}

Confira a GIF abaixo:

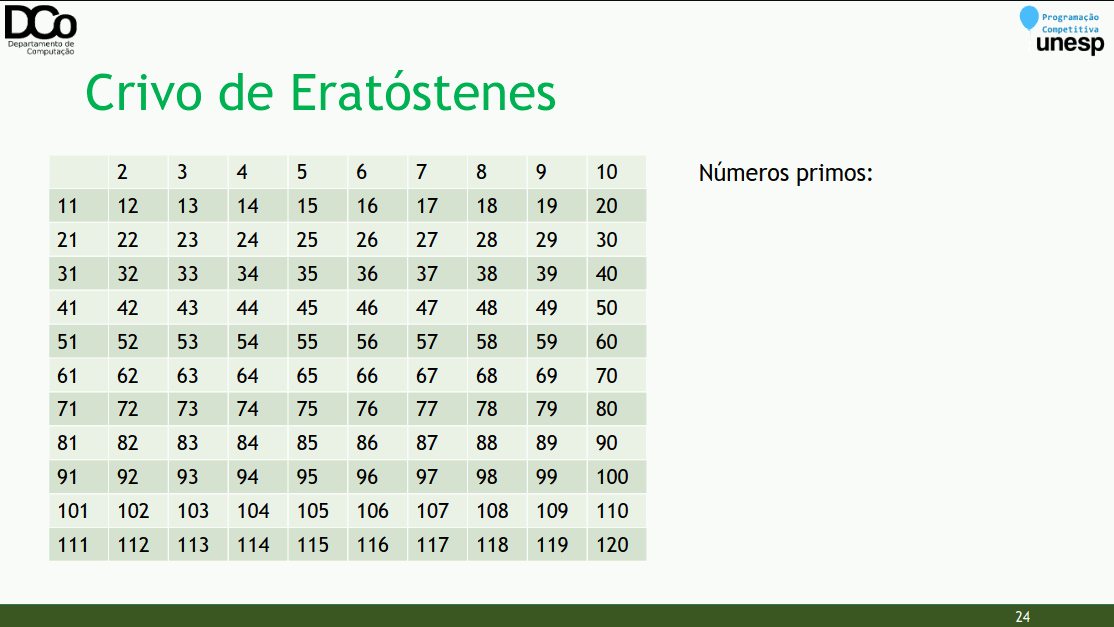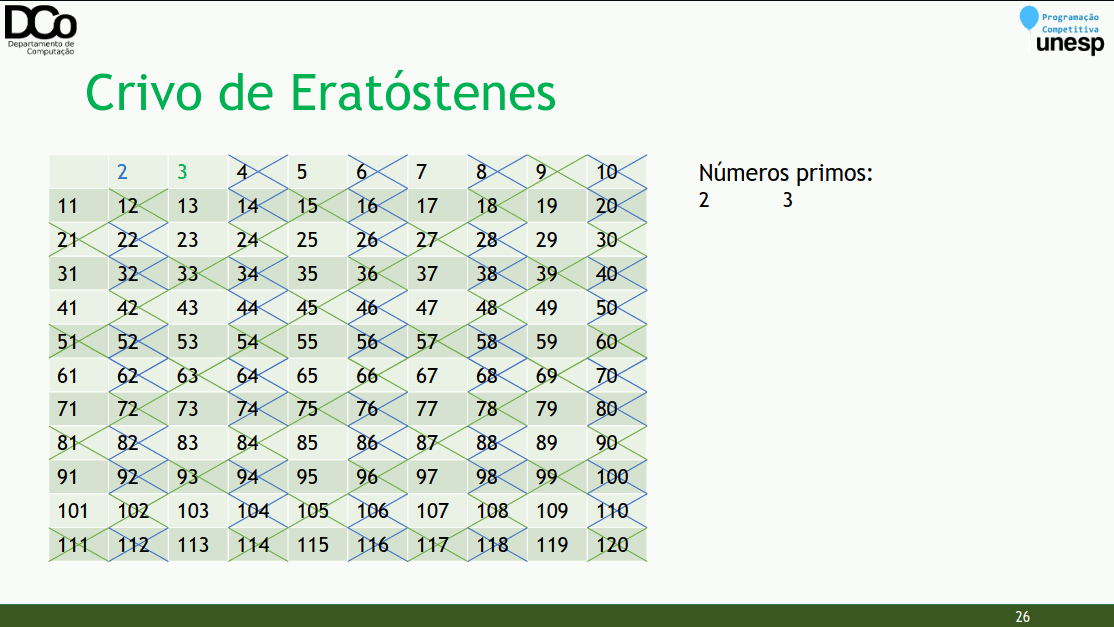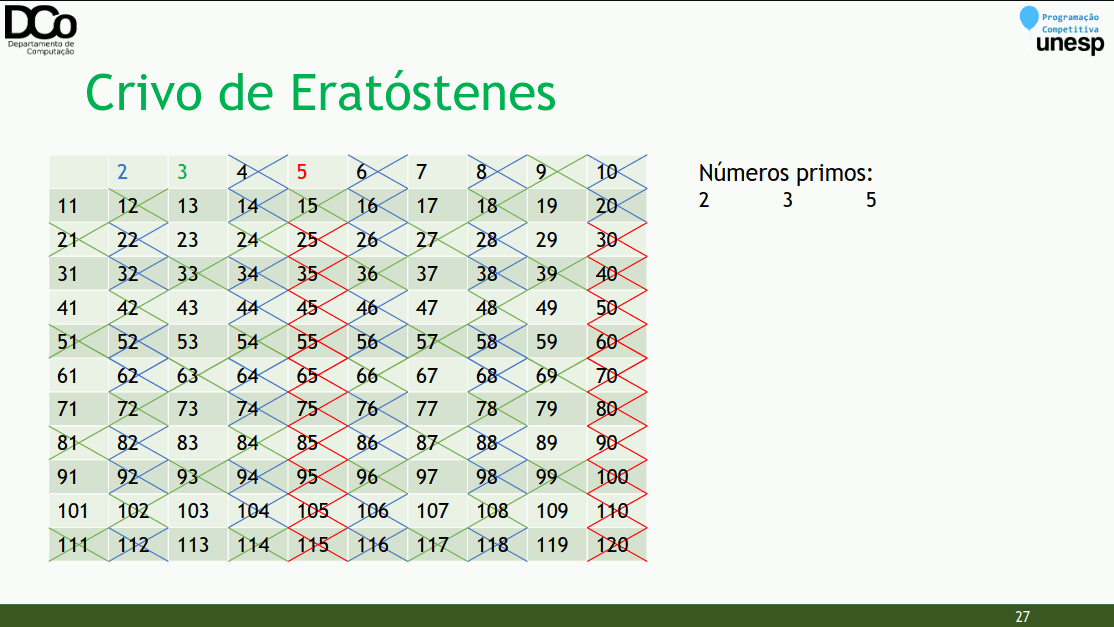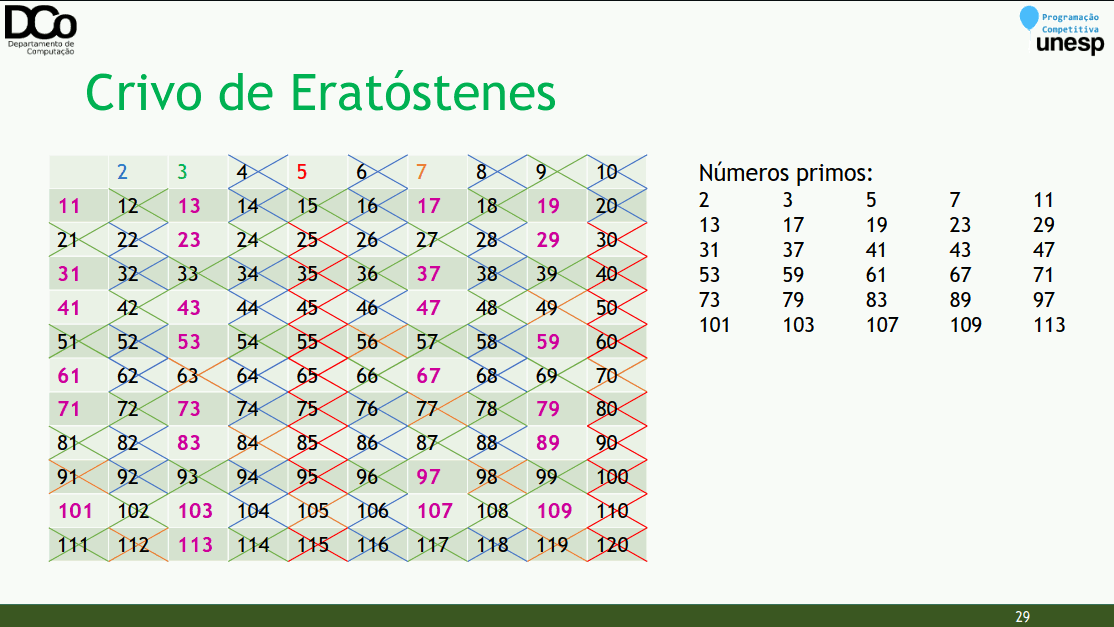
img1-img6

Este algoritmo possui complexidade 𝑂(𝑛 log log 𝑛)
Esta demonstração não é muito simples. Caso queira conferir, veja o artigo do CP-Algorithms.
Com certas otimizações ainda é possível obter um algoritmo de complexidade linear.

Fatoração

Fatoração em 𝑂(sqrt(𝑛))

vector<int> fatorar(int n) {
    vector<int> fator;
    for (int i = 2; i*i <= n; i++){
        while (n % i == 0){
            fator.push_back(i);
            n /= i;
        }
    }
    if (n > 1)
    fator.push_back(n);
    return fator;
}

Também é possível obter um algoritmo de fatoração com complexidade 𝑂(log 𝑛), baseando-se no Crivo de Eratóstenes.
Primeiramente, ao invés de utilizarmos o crivo para descobrirmos todos os primos, faremos uma pequena alteração para computar para cada número o seu Menor Fator Primo (Shortest Prime Factor - SPF).
Crivo para Fatoração

int spf[MAXN];
void crivo(){
    for(int i=2; i < MAXN; i++){
        if(spf[i] == 0){
            spf[i] = i;
            for(int j=i*i; j<MAXN; j+=i){
                if(spf[j] == 0) spf[j] = i;
            }
        }
    }
}

A partir do vetor SPF pré-calculado, podemos realizar a fatoração de um número qualquer seguindo o seguinte algoritmo:

fatores = []
enquanto n > 1
Inserir spf[n] em fatores
n = n/spf[n]

Fatoração em 𝑂(log 𝑛)

vector<int> fatorar(int n){
    vector<int> fator;
    while(n > 1){
        fator.push_back(spf[n]);
        n /= spf[n];
    }
    return fator;
}

Look-up tables

Existem casos onde podemos gerar um vetor ou matriz de consulta manualmente (ou previamente por outro programa), e inseri-los prontos no nosso código. Dessa forma, economiza-se o tempo de gerar tal vetor/matriz.
Por exemplo, se para resolver um problema precisamos de todos os primos até 𝑁, podemos embutir um vetor de primos já dentro do código.

int primos[] = {2, 3, 5, 7, 11, 13, … }

Isso também pode ser gerado por um programa auxiliar.

“The judge can’t look into your heart or your program to see your intentions - it only checks the results.” (Skiena & Revilla, 2003; p. 129)

Máximo Divisor Comum

Problema: encontrar o maior divisor comum de um par de números.
Algoritmo de Euclides
OBS: se 𝑚𝑑𝑐(𝑥, 𝑦) = 1, então dizemos que 𝑥 e 𝑦 são coprimos ou primos entre si.

MDC/GCD em 𝑂(log(𝑎 + 𝑏))

int gcd(int a, int b){
    if (a == 0)
        return b;
    return gcd(b % a, a);
}

Problema: encontrar o menor múltiplo comum entre um par de inteiros.
Para encontrar o mmc(x, y), podemos calcular o mdc(x, y) e utilizar a seguinte fórmula:

𝑚𝑚𝑐(𝑥, 𝑦) ∗ 𝑚𝑑𝑐(𝑥, 𝑦) = 𝑥 ∗ 𝑦

Ou seja:

𝑚𝑚𝑐(𝑥, 𝑦) = 𝑥 ∗ 𝑦 / 𝑚𝑑𝑐(𝑥, 𝑦)

MMC/LCM em 𝑂(log(𝑎 + 𝑏))

int lcm(int a, int b){
    return a * (b / gcd(a, b));
}

Equações diofantinas

Podemos definir uma equação diofantina linear como uma equação da forma

𝒂𝟏𝒙𝟏 + 𝒂𝟐𝒙𝟐 + ⋯ + 𝒂𝒏 𝒙𝒏 = 𝒄

sendo 𝒂𝟏, … , 𝒂𝒏 coeficientes inteiros não nulos, 𝒙𝟏 … , 𝒙𝒏 as variáveis inteiras a serem determinadas e 𝒄 uma constante inteira.
Diversos problemas podem ser modelados usando equações diofantinas.
Em especial, vamos nos preocupar com equações diofantinas de duas variáveis

𝒂𝒙 + 𝒃𝒚 = 𝒄

Equações diofantinas – Fantastic Beasts

Exemplo de Problema: Fantastic Beasts (Final da Maratona SBC de Programação - 2018)
Resumindo: considere um grafo direcionado em que os vértices representam zoológicos, e cada zoológico aponta para apenas para um outro zoológico (grau de saída = 1). Temos animais espalhados por esses zoológicos, e a cada unidade de tempo todos os animais avançam para o próximo zoológico.
Objetivo: determinar onde e quando TODOS os animais se encontrarão, no mesmo zoológico ao mesmo tempo (se isso puder ocorrer em diversos momentos e locais, determinar o primeiro deles)
Supondo que já estamos em uma fase um pouco mais avançada no problema, onde conseguimos modelar para cada zoológico z uma equação que determina os momentos em que um animal a passa por lá (os animais vão acabar presos em ciclos).

𝑡 = 𝑡0 + 𝑘. 𝑖

Proposição 1: 𝒂𝒙 + 𝒃𝒚 = 𝒄 admite solução sse 𝒈𝒄𝒅(𝒂, 𝒃) | 𝒄

==>

Sendo (𝑥0, 𝑦0) uma solução da equação
Seja 𝑑 = gcd(𝑎, 𝑏), então 𝑑|𝑎 e 𝑑|𝑏. Logo podemos reescrever 𝑎 = 𝐴𝑑 e 𝑏 = 𝐵𝑑

𝑐 = 𝑎𝑥0 + 𝑏𝑦0 = 𝐴𝑑 𝑥0 + 𝐵𝑑 𝑦0

𝑐 = 𝑑(𝐴𝑥0 + 𝐵𝑦0)

Denotando 𝑞 = 𝐴𝑥0 + 𝐵𝑦0

𝑐 = 𝑑𝑞 Portanto, 𝑑|𝑐

Proposição 1: 𝒂𝒙 + 𝒃𝒚 = 𝒄 admite solução sse 𝒈𝒄𝒅(𝒂, 𝒃) | 𝒄

<==

Seja 𝑑 = gcd(𝑎, 𝑏)
Pelo Teorema de Bézout, existe solução (𝑥0, 𝑦0) para 𝑎𝑥 + 𝑏𝑦 = 𝑑

•- Por hipótese, 𝑑|𝑐 ⇒ ∃𝑡 / 𝑐 = 𝑑𝑡

𝑐 = 𝑑𝑡

𝑐 = (𝑎𝑥0 + 𝑏𝑦0)𝑡

𝑐 = 𝑎(𝑥0𝑡) + 𝑏(𝑦0𝑡)

Portanto, se 𝑑 | 𝑐, então a equação 𝑎𝑥 + 𝑏𝑦 = 𝑐 admite solução
Como determinar uma solução?

Obter uma solução (𝑥0, 𝑦0) para 𝑎𝑥 + 𝑏𝑦 = gcd(𝑎, 𝑏)
Para 𝑎𝑥 + 𝑏𝑦 = 𝑐: a) 𝑡 = 𝑐/𝑑 em que 𝑑 = gcd(𝑎, 𝑏) b) 𝑥 = 𝑥0𝑡 c) 𝑦 = 𝑦0𝑡
Se uma equação diofantina tem uma solução, então ela tem infinitas:

Solução para 𝑎𝑥 + 𝑏𝑦 = gcd(𝑎, 𝑏)

Caso base (𝑎 = 0):
- Se 𝑎 = 0 então temos 𝑏𝑦 = gcd(0, 𝑏)
- Sabemos que gcd 0, 𝑏 = 𝑏
- Então 𝑏𝑦 = 𝑏, logo 𝑦 = 1
- Nesse caso 𝑥 pode assumir qualquer valor. Como queremos uma solução qualquer, por motivos de simplificação, faremos 𝑥 = 0

Solução base: (0, 1)
Solução para 𝑎𝑥 + 𝑏𝑦 = gcd(𝑎, 𝑏)

Passo da indução:

Temos 𝑎𝑥 + 𝑏𝑦 = gcd(𝑎, 𝑏)
Pelo Algoritmo de Euclides, sabemos que gcd 𝑎, 𝑏 = gcd 𝑏%𝑎, 𝑎 = 𝑑
Logo, podemos obter outra equação diofantina: 𝑏%𝑎 𝑥1 + 𝑎𝑦1 = 𝑑 (∗)
Solução para 𝑎𝑥 + 𝑏𝑦 = gcd(𝑎, 𝑏)
Considerando o resultado da divisão inteira, podemos dizer que:

𝑏 = 𝑏

𝑎 𝑎 + 𝑏%𝑎

𝑏%𝑎 = 𝑏 − 𝑏

𝑎 𝑎

Substituindo em (∗)

𝑏 − 𝑏

𝑎 𝑎 𝑥1 + 𝑎𝑦1 = 𝑑

𝑏𝑥1 − 𝑏

𝑎 𝑎𝑥1 + 𝑎𝑦1 = 𝑑

𝑎 𝑦1 − 𝑏

𝑎 𝑥1 + 𝑏𝑥1 = 𝑑

𝒂𝒙 + 𝒃𝒚 = 𝒅

Implementação

int gcd(int a, int b, int &x, int &y){
    if (a == 0){
        x = 0;
        y = 1;
        return b;
    }
    int x1, y1;
    int d = gcd(a, b % a, x1, y1);
    x = y1 - x1 * (b/a);
    y = x1;
    return d;
}

bool solve(int a, int b, int c, int &x0, int &y0, int &g) {
    g = gcd(abs(a), abs(b), x0, y0);
    if (c % g) {
        return false;
    }
    x0 *= c / g;
    y0 *= c / g;
    if (a < 0) x0 = -x0;
    if (b < 0) y0 = -y0;
    return true;
}

Aritmética Modular

Em vários problemas precisamos operar com os restos de divisões de inteiros.
A aritmética modular permite fazer cálculos com restos de divisões de modo eficiente, e é especialmente útil quando estamos trabalhando com números grandes (BigInteger).
Na verdade, a Aritmética Modular pode nos ajudar a evitar ter que trabalhar com números muito grandes.
A aritmética modular se baseia nas seguintes propriedades:

(𝑥 + 𝑦) % 𝑛 = ((𝑥 % 𝑛) + (𝑦 % 𝑛)) % 𝑛

(𝑥 − 𝑦) % 𝑛 = ((𝑥 % 𝑛) − (𝑦 % 𝑛)) % 𝑛

(𝑥 ∗ 𝑦) % 𝑛 = ((𝑥 % 𝑛) ∗ (𝑦 % 𝑛)) % 𝑛

(𝑥 ^ 𝑦) % 𝑛 = ((𝑥 % 𝑛) ^ 𝑦) % 𝑛

UVa 374 - Big Mod
Calcule 𝑅 = 𝐵𝑃 𝑚𝑜𝑑 𝑀
0 ≤ 𝐵, 𝑃 ≤ 2147483647 e 1 ≤ 𝑀 ≤ 46340
Parte da solução do problema UVA 374 – Big Mod

long long pow(long long x, long long y, long long mod) {
    if (y == 0)
        return 1;
    long long p = pow(x, y/2, mod);
    if (y % 2 == 0)
        return (p * p) % mod;
    else
        return (((p * p) % mod) * (x % mod)) % mod;
}

Inverso Modular

A aritmética modular não se aplica a divisão. Porém, temos o conceito de inverso multiplicativo modular.
Lembre-se que um número multiplicado pelo seu inverso é igual a 1
Da aritmética básica, sabemos que:
O inverso de um número 𝐴 é 1

𝐴